题目内容
已知函数y=mx2-6x+1(m是常数).
⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
⑵若该函数的图象与x轴只有一个交点,求m的值.
(1)证明详见解析;(2)0或9.
解析试题分析:此题考查了抛物线与x轴的交点或一次函数与x轴的交点,是典型的分类讨论思想的应用.(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1).(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;②当函数为二次函数时,利用根与系数的关系解答.
试题解析:
解:(1)∵当x=0时,y=1.
∴不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1);
(2)①当m=0时,函数y=-6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+1的图象与x轴只有一个交点,则方程mx2-6x+1=0有两个相等的实数根,
所以△=(-6)2-4m=0,m=9.
综上,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或9.
考点:抛物线与x轴的交点;一次函数图象上点的坐标特征;二次函数图象上点的坐标特征.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x > 40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?

 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点
 .
. 的值;
的值; 的图象对称轴为
的图象对称轴为 ,且过点B(-1,0).求此二次函数的表达式.
,且过点B(-1,0).求此二次函数的表达式. 与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
 .
.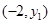 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”); ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
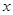 天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式; 元,试写出
元,试写出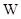 元?
元?