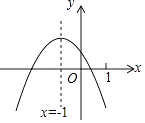��Ŀ����
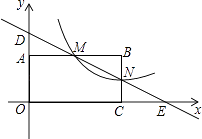
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y= ![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=
x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y= ![]() x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��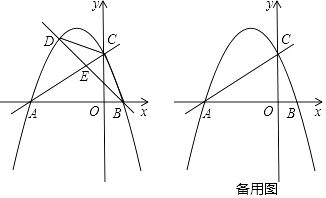
��1���������ߵĺ�������ʽ��
��2����DΪֱ��AC�Ϸ���������һ���㣻
������BC��CD����ֱ��BD���߶�AC�ڵ�E����CDE�����ΪS1 �� ��BCE�����ΪS2 �� �� ![]() �����ֵ��
�����ֵ��
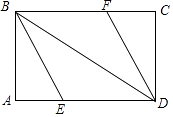
�ڹ���D��DF��AC������Ϊ��F������CD���Ƿ���ڵ�D��ʹ�á�CDF�е�ij����ǡ�õ��ڡ�BAC��2���������ڣ����D�ĺ����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺���������A����4��0����C��0��2����
��������y=�� ![]() x2+bx+c����A��C���㣬
x2+bx+c����A��C���㣬
��  ��
��
�� 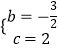 ��
��
��y=�� ![]() x2��
x2�� ![]() x+2
x+2
��2��
�⣺����ͼ��
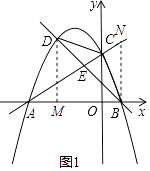
��y=0��
�ੁ ![]() x2��
x2�� ![]() x+2=0��
x+2=0��
��x1=��4��x2=1��
��B��1��0����
��D��DM��x����M����B��BN��x�ύ��AC��N��
��DM��BN��
���DME�ס�BNE��
�� ![]() =
= ![]() =
= ![]() ��
��
��D��a��=�� ![]() a2��
a2�� ![]() a+2����
a+2����
��M��a�� ![]() a+2����
a+2����
��B��1.0����
��N��1�� ![]() ����
����
�� ![]() =
= ![]() =
=  ��a+2��2+
��a+2��2+ ![]() ��
��
�൱a=2ʱ�� ![]() �����ֵ��
�����ֵ�� ![]() ��
��
�ڡ�A����4��0����B��1��0����C��0��2����
��AC=2 ![]() ��BC=
��BC= ![]() ��AB=5��
��AB=5��
��AC2+BC2=AB2��
���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P��
��P���� ![]() ��0����
��0����
��PA=PC=PB= ![]() ��
��
���CPO=2��BAC��
��tan��CPO=tan��2��BAC��= ![]() ��
��
����x���ƽ���߽�y����R����AC���ӳ�����G��
���һ����ͼ��
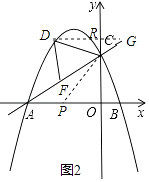
���DCF=2��BAC=��DGC+��CDG��
���CDG=��BAC��
��tan��CDG=tan��BAC= ![]() ��
��
�� ![]() ��
��
��D��a���� ![]() a2��
a2�� ![]() a+2����
a+2����
��DR=��a��RC=�� ![]() a2��
a2�� ![]() a��
a��
�� ![]() ��
��
��a1=0����ȥ����a2=��2��
��xD=��2��
����������FDC=2��BAC��
��tan��FDC= ![]() ��
��
��FC=4k��
��DF=3k��DC=5k��
��tan��DGC= ![]() =
= ![]() ��
��
��FG=6k��
��CG=2k��DG=3 ![]() k����
k����
��RC= ![]() k��RG=
k��RG= ![]() k��
k��
DR=3 ![]() k��
k�� ![]() k=
k= ![]() k��
k��
�� ![]() =
= ![]() =
= ![]() ��
��
��a1=0����ȥ����a2= ![]() ��
��
��D�ĺ�����Ϊ��2�� ![]() ��
��
����������1����������õ�A����4��0����C��0��2������y=�� ![]() x2+bx+c�����ǵõ����ۣ���2������ͼ����y=0���ⷽ�̵õ�x1=��4��x2=1�����B��1��0������D��DM��x����M����B��BN��x�ύ��AC��N���������������ε����ʼ��ɵõ����ۣ��ڸ��ݹ��ɶ������涨���õ���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P�����P����
x2+bx+c�����ǵõ����ۣ���2������ͼ����y=0���ⷽ�̵õ�x1=��4��x2=1�����B��1��0������D��DM��x����M����B��BN��x�ύ��AC��N���������������ε����ʼ��ɵõ����ۣ��ڸ��ݹ��ɶ������涨���õ���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P�����P���� ![]() ��0�����õ�PA=PC=PB=
��0�����õ�PA=PC=PB= ![]() ������x���ƽ���߽�y����R����AC��������G�����һ����ͼ����DCF=2��BAC=��DGC+��CDG�����������FDC=2��BAC����ֱ�������μ��ɵõ����ۣ�
������x���ƽ���߽�y����R����AC��������G�����һ����ͼ����DCF=2��BAC=��DGC+��CDG�����������FDC=2��BAC����ֱ�������μ��ɵõ����ۣ�
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 ��ս�п�����ϵ�д�
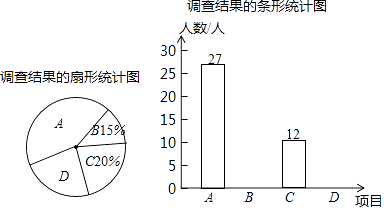
��ս�п�����ϵ�д�����Ŀ��ij������ʦ�������Լ��ν̵ļס����������������ߣ������������²�������ͳ��ͼ����
���߷��� | Ƶ�� | Ƶ�� |
152��x��155 | 3 | 0.06 |
155��x��158 | 7 | 0.14 |
158��x��161 | m | 0.28 |
161��x��164 | 13 | n |
164��x��167 | 9 | 0.18 |
167��x��170 | 3 | 0.06 |
170��x��173 | 1 | 0.02 |

��������ͳ��ͼ������������⣺
��1��ͳ�Ʊ���m= �� n= �� ����Ƶ���ֲ�ֱ��ͼ����������
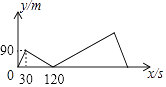
��2������β����������������ߵ���λ���ڣ���Χ�ڣ�
��3�������ߡ�167cm��4���У��ס����������2�ˣ��ִ�4���������ѡ2�˲��䵽ѧУ���커�����У������б�����״ͼ�ķ�����������˶�������ͬ�༶�ĸ��ʣ�