题目内容
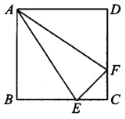
【题目】如图所示,正方形ABCD的边长为4 ![]() ,E、F分别是BC、DC边上一动点,E、F同时从点C均以1
,E、F分别是BC、DC边上一动点,E、F同时从点C均以1 ![]() 的速度分别向点B、点D运动,当点E与点B重合时,运动停止.设运动时间为
的速度分别向点B、点D运动,当点E与点B重合时,运动停止.设运动时间为![]() (
(![]() ),运动过程中△AEF的面积为
),运动过程中△AEF的面积为![]() ,请写出用
,请写出用![]() 表示
表示![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
【答案】y![]()
【解析】
△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,分别表示正方形ABCD的面积、△ABE的面积、△ADF的面积、△ECF的面积代入即可.
设运动时间为x(s),
∵点E,F同时从点C出发,以每秒21cm的速度分别向点B,D运动,
∴CE=x,CF=x,BE=4-x,DF=4-x,
∴△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,
即:y=16-![]() ABBE-
ABBE-![]() ADDF-
ADDF-![]() ECFC
ECFC
=16-![]() 4(4-x)-
4(4-x)-![]() 4(4-x)-
4(4-x)-![]() xx
xx
=![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目