题目内容
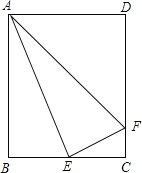
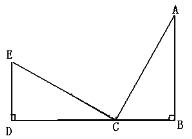
【题目】如图,已知AB⊥BD于B,ED⊥BD于D,EC⊥AC,AC=EC,若DE=2,AB=4,则DB=______.
【答案】6;
【解析】
由垂直的定义得到∠EDC=∠ABC=∠ACE=90°,再根据等角的余角相等得到∠E=∠ACB,而AC=EC,根据三角形全等的条件得到Rt△EDC≌Rt△CBA,则DE=BC=2,DC=AB=4,即可得到DB.
解:∵AB⊥BD,ED⊥BD,EC⊥AC,
∴∠EDC=∠ABC=∠ACE=90°,
∴∠E+∠ECD=90°,∠ECD+∠ACB=90°,
∴∠E=∠ACB,
而AC=EC,
∴Rt△EDC≌Rt△CBA,
∴DE=BC,DC=AB,
而DE=2,AB=4,
∴BC=2,DC=4,
∴DB=2+4=6.
故答案为:6.

练习册系列答案
相关题目