��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���֪![]() ��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1������C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0����1������C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
��1����ͼ���������߾���A��B���㣬�������ߵĽ���ʽ��
��2��ƽ��1�е������ߣ�ʹ����P��ֱ��AC�ϲ���AC��������Ϊ![]() ʱ����֤����ƽ�ƺ����������ֱ��AC����x���ϵ�ͬһ�㣮
ʱ����֤����ƽ�ƺ����������ֱ��AC����x���ϵ�ͬһ�㣮
��3����2������£�����AC�������⻬��ʱ������������ֱ��AC����һ����ΪQ��ȡBC���е�N����̽��NP+BQ�Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
����𡿽⣺�ߵ���ֱ��������ABC�Ķ���A������Ϊ��0����1����C������Ϊ��4��3��
���B��������4����1����
�������߹�A��0����1����B��4����1�����㣬
��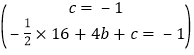 ��
��
��ã�b=2��c=��1��
�������ߵĺ�������ʽΪ��![]() .
.
��2��
�����ͼ2���趥��P��ֱ��AC�ϲ���AC��������![]() ʱ������P�䣬��P��M��y�ᣬPM��x�ᣬ����M�㣬
ʱ������P�䣬��P��M��y�ᣬPM��x�ᣬ����M�㣬
�ߵ�A������Ϊ��0����1������C������Ϊ��4��3����
��ֱ��AC�Ľ���ʽΪy=x��1��
��ֱ�ߵ�б��Ϊ1��
���P��PM�ǵ���ֱ�������Σ�
��PP��=![]() ��
��
��P��M=PM=1��
������������ƽ��1����λ������ƽ��1����λ��
��![]() =
=![]() ��
��
��ƽ�ƺ�������ߵĽ���ʽΪ![]() ��
��
��y=0����0=![]() ��
��
���x1=1��x=52��
��ƽ�ƺ����������x��Ľ���Ϊ��1��0������5��0����
��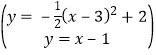 ����
����![]() ��
��![]()
��ƽ�ƺ����������AC�Ľ���Ϊ��1��0����
��ƽ�ƺ����������ֱ��AC����x���ϵ�ͬһ�㣨1��0����
��3��
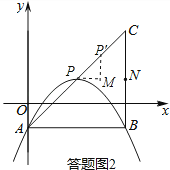
���ͼ3��ȡ��B����AC�ĶԳƵ�B�䣬�õ�B�������Ϊ��0��3����BQ=B��Q��ȡAB�е�F��
����QF��FN��QB�䣬��FN��PQ����FN=PQ��
���ı���PQFNΪƽ���ı��Σ�
��NP=FQ��
��NP+BQ=FQ+B��Q��FB��=![]() =
=![]() ��
��
�൱B�䡢Q��F���㹲��ʱ��NP+BQ��С����СֵΪ![]() ��
��
����������1���������B�����꣬Ȼ�����ô���ϵ������������ߵĺ�������ʽ��
��2�������ͼ2���趥��P��ֱ��AC�ϲ���AC��������![]() ʱ������P�䣬��P��M��y�ᣬPM��x�ᣬ����M�㣬����ֱ��AC��б����á�P��PM�ǵ���ֱ�������Σ������������������ƽ��1����λ������ƽ��1����λ���Ӷ����ƽ�ƺ�Ľ���ʽ�����������x��Ľ��㣬��ֱ��AC�Ľ��㣬����֤�ý��ۣ�
ʱ������P�䣬��P��M��y�ᣬPM��x�ᣬ����M�㣬����ֱ��AC��б����á�P��PM�ǵ���ֱ�������Σ������������������ƽ��1����λ������ƽ��1����λ���Ӷ����ƽ�ƺ�Ľ���ʽ�����������x��Ľ��㣬��ֱ��AC�Ľ��㣬����֤�ý��ۣ�
��3�����ͼ3��ʾ������B����ֱ��AC�ĶԳƵ�B�䣬�ɷ�����֪����B�䡢Q��F��AB�е㣩���㹲��ʱ��NP+BQ��С����СֵΪ�߶�B��F�ij��ȣ�

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�����Ŀ��ijУ��չУ���������ꡱ��ѡ������С�����Ϊ�֡�������ǿ����������Т�ϰ��ס�������ʵ���š��������ÿλͬѧֻ�ܲ�������һ�࣬��ѡ��������ѡ��20λУ���������ꡱ����ͳ�ƣ�����������ͳ�Ʊ����������֣�ͳ�Ʊ���ǰ���е����ݶ�����ȷ�ģ������е���������һ���Ǵ���ģ�
��� | Ƶ�� | Ƶ�� |
�������������� | a | 0.20 |
��ǿ������������ | 3 | b |
Т�ϰ����������� | 7 | 0.35 |
��ʵ������������ | 6 | 0.32 |
����������Ϣ������������⣺
��1��ͳ�Ʊ��е�a= ��b ;
��2��ͳ�Ʊ������д���������� �������ݵ���ȷֵ�� ;
��3��УС���߾�����A��B��C��λ����ǿ�����������ꡱ������ɷ���λ���û���״ͼ���б��ķ�������A��B�����ɷõ��ĸ���






