Question

【题目】如图，AB是⊙O的切线，B为切点，AC经过点O，与⊙O分别相交于点D，C．若∠ACB=30°，AB= ，则阴影部分的面积是（　　）

A.
B.
C.﹣
D.﹣

Answer 1

【答案】C
【解析】解：连接OB．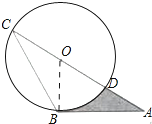

∵AB是⊙O切线，
∴OB⊥AB，
∵OC=OB，∠C=30°，
∴∠C=∠OBC=30°，
∴∠AOB=∠C+∠OBC=60°，
在RT△ABO中，∵∠ABO=90°，AB= ，∠A=30°，
∴OB=1，
∴S阴=S△ABO﹣S扇形OBD= ×1× ﹣ = ﹣ ．
故选C．
【考点精析】本题主要考查了切线的性质定理和扇形面积计算公式的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．