Question

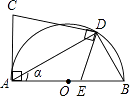
【题目】如图，将一矩形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG．若AB=4，BC=8，则△ABF的面积为 ．

Answer 1

【答案】6
【解析】解：∵将一矩形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG，
∴FG是AC的垂直平分线，
∴AF=CF，
设AF=FC=x，
在Rt△ABF中，有勾股定理得：AB2+BF2=AF2 ，
42+（8﹣x）2=x2 ，
解得：x=5，
即CF=5，BF=8﹣5=3，
∴△ABF的面积为 ×3×4=6，
故答案为：6．
根据折叠的性质求出AF=CF，根据勾股定理得出关于CF的方程，求出CF，求出BF，根据面积公式求出即可．本题考查了矩形的性质，折叠的性质，勾股定理的应用，能得出关于x的方程是解此题的关键．