题目内容
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF.求证: 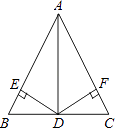
(1)AD是△ABC的角平分线;
(2)AE=AF.
【答案】
(1)证明:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BED和△CFD都是直角三角形,
在Rt△BED与Rt△CFD中,
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∴AD是△ABC的角平分线
(2)证明:∵Rt△BED≌Rt△CFD,
∴∠B=∠C,
∴AB=AC,
∵BE=CF,
∴AE=AF
【解析】(1)根据HL可证Rt△BED≌Rt△CFD,根据全等三角形的性质可得DE=DF,再根据角平分线的判定即可求解;(2)根据全等三角形的性质可得∠B=∠C,根据等角对等边可得AB=AC,再根据线段的和差求解即可.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目