题目内容
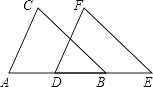
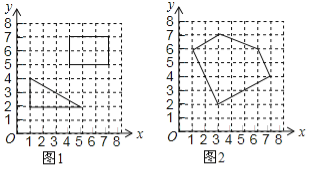
【题目】“皮克定理”是用来计算顶点在整点的多边形面积的公式，公式表达式为
，孔明只记得公式中的S表示多边形的面积，a和b中有一个表示多边形边上（含顶点）的整点个数，另一个表示多边形内部的整点个数，但不记得究竟是a还是b表示多边形内部的整点个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部的整点个数的字母是 ，并运用这个公式求得图2中多边形的面积是 ．
【答案】a，17.5．
【解析】
试题分析：如图1，∵三角形内由1个格点，边上有8个格点，面积为4，即4=1+
﹣1；
矩形内由2个格点，边上有10个格点，面积为6，即6=2+
﹣1；
∴公式中表示多边形内部整点个数的字母是a；
图2中，a=15，b=7，故S=15+
﹣1=17.5．
故答案为：a，17.5．
能考试期末冲刺卷系列答案【题目】农业部门引进一批新麦种，在播种前做了五次发芽试验，目的是想了解一粒这样的麦种发芽情况，实验统计数据如下：
实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
估计在与实验条件相同的情况下，种一粒这样的麦种发芽的概率约为
【题目】“节能环保，低碳生活”是我们倡导的一种生活方式，某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台，三种家电的进价和售价如表所示：
价格 | 进价 | 售价 |
电视机 | 5000 | 5500 |
洗衣机 | 2000 | 2160 |
空 调 | 2400 | 2700 |
（1）在不超出现有资金的前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的3倍．请问商场有哪几种进货方案？
（2）在“2012年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动．在（1）的条件下，若三种电器在活动期间全部售出，商家预估最多送出多少张？
