题目内容
【题目】“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:
价格 | 进价 | 售价 |
电视机 | 5000 | 5500 |
洗衣机 | 2000 | 2160 |
空 调 | 2400 | 2700 |
(1)在不超出现有资金的前提下,若购进电视机的数量和洗衣机的数量相同,空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案?
(2)在“2012年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在(1)的条件下,若三种电器在活动期间全部售出,商家预估最多送出多少张?
【答案】
(1)解:设购进电视机x台,则洗衣机是x台,空调是(40﹣2x)台,
根据题意得: 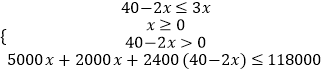 ,
,
解得:8≤x≤10,
根据x是整数,则从8到10共有3个正整数,分别是8、9、10,因而有3种方案:
方案一:电视机8台、洗衣机8台、空调24台;
方案二:电视机9台、洗衣机9台、空调22台;
方案三:电视机10台、洗衣机10台、空调20台.
(2)解:三种电器在活动期间全部售出的金额y=5500x+2160x+2700(40﹣2x),
即y=2260x+108000.
由一次函数性质可知:当x=10最大时,y的值最大值是:2260×10+108000=130600(元).
由现金每购1000元送50元家电消费券一张,可知130600元的销售总额最多送出130张消费券.
【解析】(1)设购进电视机x台,则洗衣机是x台,空调是(40-2x)台,根据空调的数量不超过电视机的数量的3倍,且x以及40-2x都是非负整数,即可确定x的范围,从而确定进货方案;
(2)三种电器在活动期间全部售出的金额,可以表示成x的函数,根据函数的性质,即可确定y的最大值,从而确定所要送出的消费券的最大数目.