题目内容
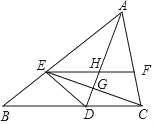
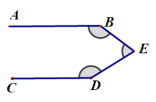
【题目】[感知发现]：如图，是一个“猪手”图，AB∥CD，点E在两平行线之间，连接BE，DE ，我们发现：∠E=∠B+∠D
证明如下：过E点作EF∥AB．
∠B=∠1(两直线平行，内错角相等．）
又
AB∥CD(已知）
CD∥EF(如果两条直线都与第三条直线平行，那么这两条直线也互相平行．）
∠2=∠D(两直线平行，内错角相等．）
∠1+∠2=∠B+∠D(等式的性质1．）
即：∠E=∠B+∠D
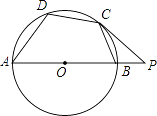
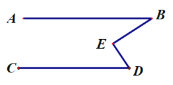
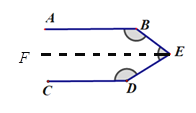
[类比探究]：如图是一个“子弹头”图，AB∥CD，点E在两平行线之间，连接BE，DE．试探究∠E+∠B+∠D=360°．写出证明过程．
[创新应用]：
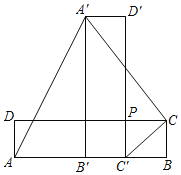
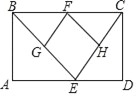
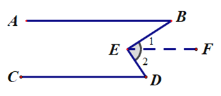
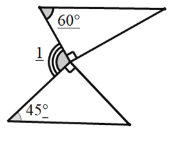
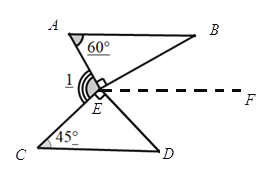
(1)．如图一，是两块三角板按如图所示的方式摆放，使直角顶点重合，斜边平行，请直接写出∠1的度数．
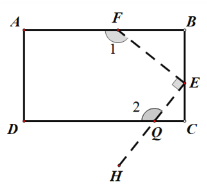
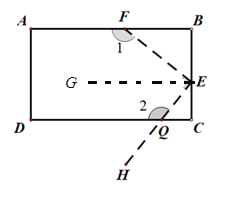
(2)．如图二，将一个长方形ABCD按如图的虚线剪下，使∠1=120
，∠FEQ=90°． 请直接写出∠2的度数．
【答案】类比探究：见解析；
创新应用：(1)：
创新应用：(2)：
【解析】
[类比探究]：如图，过
作
结合已知条件得
利用平行线的性质可得答案，
[创新应用]：
(1)：由题意得：
过作 得到
利用平行线的性质可得答案，
(2)：由题意得： 过作
得到 
利用平行线的性质可得答案．
解：类比探究：如图，过作
[创新应用]：(1)：由题意得： 过作
(2)：由题意得： 过作
，
∠1=120
，∠FEQ=90°，
练习册系列答案
相关题目
