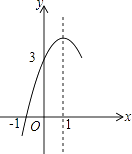题目内容
【题目】(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.

【答案】(1)作图见解析;(2)证明见解析;(3)m=![]() .
.
【解析】
试题本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
(1)将函数y=|x|,变形为y=x(x≥0),y=﹣x(x≤0),然后利用两点法画出函数图象即可;
(2)将函数解析式变形为:y=(x﹣2)+2,从而可知直线经过点(2,2);
(3)首先由勾股定理求得OC的长,然后根据三角形的面积为2,可求得OD的长度,从而可得到点D的坐标,将点D的坐标代入函数解析式可求得m的值.
试题解析:解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),将x=0代入得:y=0;将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),将x=0代入得:y=0;将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点0(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
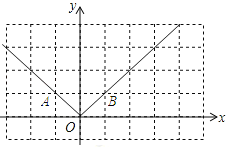
(2)∵y=mx﹣2(m﹣1)=m(x﹣2)+2,
∴x﹣2=0,y=2
∴x=2,y=2,
即函数图象过定点(2,2)…(6分)
(3)如下图:
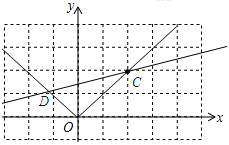
∵函数y=mx﹣2(m﹣1)的图象经过顶点(2,2)
∴OC=![]() =2
=2![]() .
.
∴![]() ODOC=2,
ODOC=2,
∴OD=![]() ,
,
所以点D的坐标为(﹣1,1).
将x=﹣1,y=1代入y=mx﹣2(m﹣1)得:m=![]() .
.

练习册系列答案
相关题目