题目内容
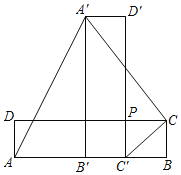
【题目】如图,在长方形ABCD中,AB=a,BC=b(a>2b),点P在边CD上,且PC=BC,长方形ABCD绕点P顺时针旋转90°后得到长方形A'B'C'D'(点B'、C'落在边AB上),请用a、b的代数式分别表示下列图形的面积.
(1)三角形PCC'的面积S1;
(2)四边形AA'CC'的面积S,并化简.
【答案】(1)△PCC'的面积S1=![]() b2;(2)
b2;(2)![]() +
+![]()
【解析】
(1)依据△PCC'是等腰直角三角形,即可得出△PCC'的面积S1=![]() b2;
b2;
(2)依据△BCC'是等腰直角三角形,可得BC'=BC=b,BB'=2b,进而得到AB'=a-2b,再根据四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'进行计算即可.
(1)由旋转可得,PC=PC'=b,∠CPC'=90°,

∴△PCC'是等腰直角三角形,
∴△PCC'的面积S1=![]() b2;
b2;
(2)由题可得,∠BCC'=45°,∠B=90°,A'B'=AB=a,
∴∠BCC'=∠BC'C=45°,
∴△BCC'是等腰直角三角形,
∴BC'=BC=b,BB'=2b,
∴AB'=a-b-b=a-2b,
∴四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'
=![]() a(a-2b)+
a(a-2b)+![]() -
-![]()
=![]() -ab+ab+b2-
-ab+ab+b2-![]()
=![]() +
+![]() .
.

练习册系列答案
相关题目