题目内容
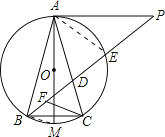
【题目】如图,⊙O是△ABC的外接圆,AM是⊙O的直径,过点A作AP⊥AM.

(1)求证:∠PAC=∠ABC.
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为BC的中点,且∠DCF=∠P,求证:![]() =
=![]() .
.
【答案】见解析
【解析】
试题分析:(1)连接BM,由圆周角定理和垂直的性质即可证明∠PAC=∠ABC;
(2)连接AE,根据垂径定理得出AM⊥BC,进而得出AP∥BC,得出△ADE∽△CDF,根据相似三角形的性质:对应边的比值相等即可得出![]() .
.
证明:
(1)连接BM,
∵AM是直径,
∴∠ABM=90°
又∵AP⊥AM,
∴∠ABC+∠CBM=∠PAC+∠CAM=90°,
又∵∠CBM=∠CAM,
∴∠PAC=∠ABC;
(2)连接AE,
∵AM是直径,M为BC的中点
∴BC⊥AM,
又∵AP⊥AM,
∴AP∥BC,
∴∠DCF=∠P=∠PBC=∠EAC,
又∵∠CDF=∠ADE,
∴△ADE∽△CDF,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目