题目内容
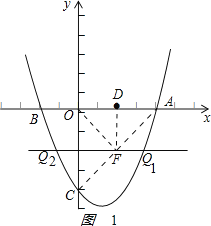
【题目】已知：如图1，二次函数y=ax2﹣2ax+c（a＞0）的图象与y轴交于点C（0，﹣4），与x轴交于点A、B两点，点A的坐标为（4，0）．
（1）求该抛物线的函数解析式；
（2）点P（t，0）是线段OB上一动点（不与O、B重合），点E是线段BC上的点，以点B、P、E为顶点的三角形与三角形ABC相似，连结CP，求△CPE的面积S与t的函数关系式；
（3）如图2，若平行于x轴的动直线与该抛物线交于点Q，与直线AC交于点F，点D的坐标为（2，0），则存在这样的直线，使得△ODF为等腰三角形，请直接写出点Q坐标．
【答案】（1）y=
x2﹣x﹣4；（2）S=﹣
t2﹣
t+
；（3）存在这样的直线l，使得△ODF是等腰三角形，点Q的坐标为：Q1（1+
，﹣2）或Q2（1﹣，﹣2）或Q3（1+
，﹣3）或Q4（1﹣，﹣3）．
【解析】
试题分析：（1）根据待定系数法，可得函数解析式；
（2）可先设P的坐标为（m，0）；根据相似三角形的性质，可得S△BEP，根据S△CPE=S△BOC﹣S△BPE﹣SOPC，可得函数关系式；
（3）本题要分三种情况进行求解：①当OD=OF时，根据等腰直角三角形，可得出F的坐标应该是（2，2），根据F的纵坐标代入抛物线的解析式中即可求出Q的坐标；②当OF=DF时，根据线段垂直平分线的性质，可得OM=1，根据等腰直角三角形的性质，可得FM=AM=3，也就得出了F的纵坐标，根据①的方法求出Q的坐标；③当OD=OF时，OF=2，由于O到AC的最短距离为2
，因此此种情况是不成立的，综合上面的情况即可得出符合条件的P的坐标
解：（1）把C（0，﹣4）和A（4，0）代入y=ax2﹣2ax+c（a＞0）得，
，解得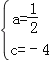
解析式为y=x2﹣x﹣4；
（2）BP=t+2，OP=﹣t，S△ABC=4×6÷2=12，S△OPC=4×（﹣t）÷2=2t，
①△BPE∽△BAC，则
=
，
则
=（
）2，S△BPE=（）2×12=
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣
﹣（﹣2t）=﹣
t2+
t+
②△BEP∽△BAC，则
=
，
则
=（）2，S△BEP=（
）2×12=
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣﹣（﹣2t）=﹣t2﹣t+
（3）存在这样的直线，使得△ODF是等腰三角形，理由为：
在△ODF中，分三种情况考虑：
①若DO=DF，如图1：
，
∵A（4，0），D（2，0），
∴AD=OD=DF=2，
又在Rt△AOC中，OA=OC=4，
∴∠OAC=45°，
∴∠DFA=∠OAC=45°，
∴∠ADF=90°，
此时，点F的坐标为（2，﹣2），
由
x2﹣x﹣4=﹣2，
解得：x1=1+
，x2=1﹣，
此时，点P的坐标为：P（1+，﹣2）或P（1﹣，﹣2）；
②若FO=FD，过点F作FM⊥x轴于点M，如图2：
，
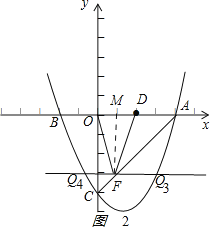由等腰三角形的性质得：OM=
OD=1，
∴AM=3，
∴在等腰直角△AMF中，MF=AM=3，
∴F（1，3），
由x2﹣x﹣4=﹣3，
解得：x1=1+
，x2=1﹣，
此时，点P的坐标为：P（1+，﹣3）或P（1﹣，﹣3）；
③若OD=OF，
∵OA=OC=4，且∠AOC=90°，
∴AC=4 
，
∴点O到AC的距离为2√2，而OF=OD=2＜2√2，与OF≥2√2矛盾，
所以AC上不存在点使得OF=OD=2，
此时，不存在这样的直线l，使得△ODF是等腰三角形；
综上所述，存在这样的直线l，使得△ODF是等腰三角形，点Q的坐标为：Q1（1+，﹣2）或Q2（1﹣，﹣2）或Q3（1+，﹣3）或Q4（1﹣，﹣3）．
