题目内容
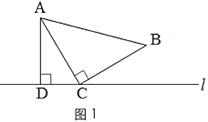
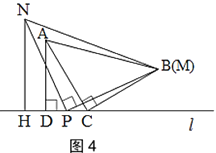
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
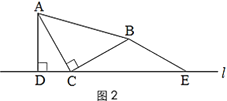
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
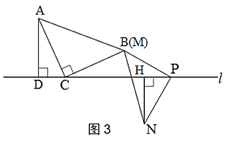
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


【答案】(1)证明见解析;(2)当点D运动到BC中点(H点)时,AC⊥DE.理由见解析;(3)∠ADB的度数为20°或40°或100°.
【解析】
(1)由∠DAE=∠BAC证明∠BAD=∠CAE,再证明△BAD≌△CAE即可得到结论,
(2)利用等腰三角形的性质,证明∠CAH=∠CAE,再利用三线合一可得结论,
(3)分三种情形:①当点D在CB的延长线上时,∠ADB=40°; ②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ADB=180°-20°-60°=100°. ③当点D在BC 延长线上时,最小角只能是∠ADB=20°;即可得到答案.
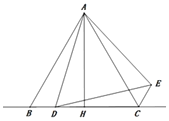
证明:(1)如图1.
∵∠DAE=∠BAC
∴∠BAD=∠CAE
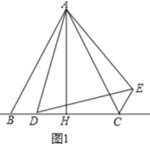
在△BAD和△CAE中,
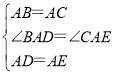 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)当点D运动到BC中点(H点)时,AC⊥DE
理由是:如图2.
∵AB=AC,AH⊥BC
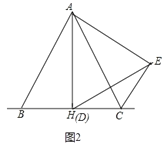
∴∠BAH=∠CAH
∵∠BAH=∠CAE,
∴∠CAH=∠CAE
∵AH=AE,
∴AC⊥DE.
(3)∠ADB的度数为20°或40°或100°.
理由如下:
①如图3中,当点D在CB的延长线上时,
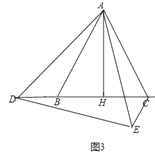
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC.
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+∠EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,∴△ABC是等边三角形,
∴∠ABC=60°
∵△ABD中的最小角是∠BAD=20°,
则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,
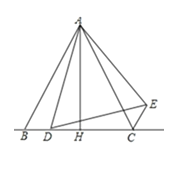
同理可得:∠ADB=180°-20°-60°=100°.
③当点D在BC延长线上时,最小角只能是∠ADB=20°,
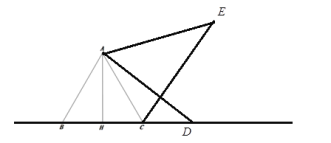
综上所述:满足条件的∠ABD的值为20°或40°或100°.

 期末集结号系列答案
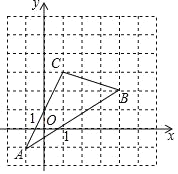
期末集结号系列答案【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标;
(2)求出△ABC的面积S△ABC.
【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.