Question

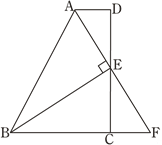
【题目】（1）如图①，在四边形中，，点是的中点，若是的平分线，试判断，，之间的等量关系．

解决此问题可以用如下方法：延长交的延长线于点，易证得到，从而把，，转化在一个三角形中即可判断．

，，之间的等量关系________；

（2）问题探究：如图②，在四边形中，，与的延长线交于点，点是的中点，若是的平分线，试探究，，之间的等量关系，并证明你的结论．

Answer 1

【答案】（1）；（2），理由详见解析.

【解析】

（1）先根据角平分线的定义和平行线的性质证得，再根据AAS证得≌，于是，进一步即得结论；

（2）延长交的延长线于点，如图②，先根据AAS证明≌，可得，再根据角平分线的定义和平行线的性质证得，进而得出结论.

解：（1）.

理由如下：如图①，∵是的平分线，∴

∵，∴，∴，∴.

∵点是的中点，∴，

又∵，

∴≌（AAS），∴.

∴.

故答案为：.

（2）.

理由如下：如图②，延长交的延长线于点.

∵，∴，

又∵，，

∴≌（AAS），∴，

∵是的平分线，∴，

∵，∴，∴，

∵，∴.