题目内容
【题目】某医院医生为了研究该院某种疾病的诊断情况,需要调查来院就诊的病人的两个生理指标![]() ,
,![]() ,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
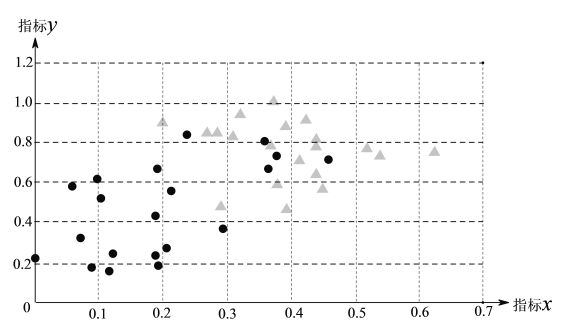
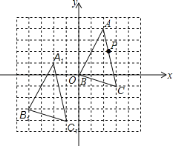
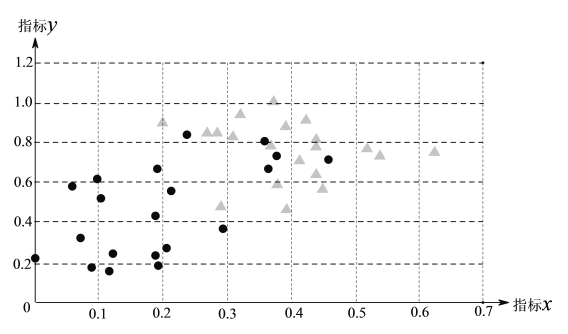
注“●”表示患者,“▲”表示非患者.
根据以上信息,回答下列问题:
(1)在这40名被调查者中,
①指标![]() 低于0.4的有 人;
低于0.4的有 人;
②将20名患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,20名非患者的指标
,20名非患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,则
,则![]()
![]() ,
,![]()
![]() (填“>”,“=”或“<”);
(填“>”,“=”或“<”);
(2)来该院就诊的500名未患这种疾病的人中,估计指标![]() 低于0.3的大约有 人;
低于0.3的大约有 人;
(3)若将“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
【答案】(1)①9;② <,>;(2)100;(3)0.25
【解析】
(1)①直接统计指标![]() 低于0.4的有人的个数即可;
低于0.4的有人的个数即可;
②通过观察图表估算出指标![]() 、
、![]() 的平均数,然后再进行比较即可确定平均数的大小;根据点的分散程度可以确定方差的大小关系.
的平均数,然后再进行比较即可确定平均数的大小;根据点的分散程度可以确定方差的大小关系.
(2)先估算出样本中未患这种疾病的人中指标![]() 低于0.3的概率,然后500乘以该概率即可;
低于0.3的概率,然后500乘以该概率即可;
(3)通过观察统计图确定不在“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”范围内且患病的人数,最后用概率公式求解即可.
低于0.8”范围内且患病的人数,最后用概率公式求解即可.
解:(1)①经统计指标![]() 低于0.4的有9人 ,故答案为9;
低于0.4的有9人 ,故答案为9;
②观察统计图可以发现,![]() 大约在0.3左右,
大约在0.3左右,![]() 大约在0.6左右,故
大约在0.6左右,故![]() <
<![]() ;
;
观察图表可以发现,x指标的离散程度大于y指标,故![]() >
>![]() ;
;
故答案为<、>;
(2)由统计图可知:在20名未患病的样本中,指标![]() 低于0.3的大约有4人,则概率为
低于0.3的大约有4人,则概率为![]() ;所以的500名未患这种疾病的人中,估计指标
;所以的500名未患这种疾病的人中,估计指标![]() 低于0.3的大约有500×
低于0.3的大约有500×![]() =100人.
=100人.
故答案为100;
(3)通过统计图可以发现有五名患病者没在“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”,漏判;则被漏判的概率为
低于0.8”,漏判;则被漏判的概率为![]() =0.25.
=0.25.
答:被漏判的概率为0.25.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案