题目内容
【题目】(阅读)
如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,8];
(尝试)
(1)若点D与OA的中点重合,则这个操作过程为FZ[____,____];
(2)若点D恰为AB的中点(如图2),求θ的值;
(应用)
经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l与AB相交于点F,试画出图形并解决下列问题:
①求出a的值;
②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.
(备注:等腰直角三角形的三边关系满足![]() 或
或![]() )
)
【答案】(1)FZ[45°,16];(2)θ=30°;【应用】①a的值为14;② ![]() .
.
【解析】
(1)利用轴对称的性质,即可解决问题;
(2)延长MD、OA,交于点N,如图2.易证△BDM≌△AND,则有DM=DN,根据垂直平分线的性质,可得OM=ON,根据等腰三角形的性质,可得∠MOD=∠NOD,从而可求出θ.
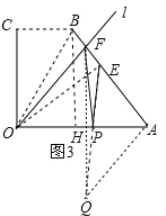
(3)①过点B作BH⊥OA于点H,如图3,易得∠FOA=45°,∠OFA=90°,∠OAB=45°,
从而得∠HBA=∠HAB,则有BH=AH,易证四边形BCOH是平行四边形,则有BH=CO=8,OH=CB=6,即可求出OA的长,进而求出a的值;②过点F作OA的对称点Q,连接AQ,EQ,如图3,则有∠QAO=∠FAO=45°,QA=FA,从而可得∠QAF=90°,然后根据等腰直角三角形三边的比例,求得:AB,AF,进而,求得BF,EF,AE,在RtQAE中,根据勾股定理,可求出EQ的长,最后根据两点之间线段最短,可知:当E,P,Q三点共线时,PE+PF=PE+PQ最小,最小值为线段EQ长,即可.
(1)∵点D与OA的中点重合,
∴θ=![]() ,a=OA=2OC=2×8=16,
,a=OA=2OC=2×8=16,
∴这个操作过程为FZ[45°,16];
(2)延长MD、OA,交于点N,如图2.
∵∠AOC=∠BCO=90°,
∴∠AOC+∠BCO=180°,
∴BC∥OA,
∴∠B=∠DAN.
在△BDM和△ADN中,
 ,
,
∴△BDM≌△ADN(ASA),
∴DM=DN.
∵∠ODM=∠OCM=90°,
∴根据线段垂直平分线的性质可得OM=ON,
∴根据等腰三角形的性质可得∠MOD=∠NOD.
由折叠可得∠MOD=∠MOC=θ,
∴∠COA=3θ=90°,
∴θ=30°
(3)①过点B作BH⊥OA于点H,如图3.
∵∠COA=90°,∠COF=45°,
∴∠FOA=45°.
∵点B与点E关于直线l对称,
∴∠OFA=∠OFB=90°,
∴∠OAB=45°,
∴∠HBA=90°﹣45°=45°=∠HAB,
∴BH=AH.
∵CO⊥OA,BH⊥OA,∴CO∥BH.
∵BC∥OA,∴四边形BCOH是平行四边形,
∴BH=CO=8,OH=CB=6,
∴OA=OH+AH=OH+BH=6+8=14.
∴a的值为14.
②过点F作OA的对称点Q,连接AQ,EQ,如图3,
则有∠QAO=∠FAO=45°,QA=FA,
∴∠QAF=90°,
在等腰RtBHA中,![]() ,
,
在等腰RtOFA中,![]() ,
,
∴BF=AB-AF=![]() ,
,
由折叠的性质,可得:EF=BF=![]() ,
,
∴AE=AF-EF=![]() .
.
在RtQAE中,![]()
![]() .
.
根据两点之间线段最短,可知:当E,P,Q三点共线时,PE+PF=PE+PQ最小,最小值为线段EQ长,
∴PE+PF的最小值为![]() .
.