题目内容
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为的切线,
为的切线,![]() 、
、![]() 为切点,连接
为切点,连接![]() 、
、![]() ,
,![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,给出下列结论:①
,给出下列结论:①![]() ;②点
;②点![]() 为
为![]() 的内心;③
的内心;③![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
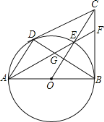
A. ① B. ①② C. ①②③ D. ①②③④
【答案】C
【解析】
①根据切线长定理,证△COB≌△COD,可得∠DCO=∠BCO.故OC⊥BD.根据圆周角定理即可得出AD⊥BD,由此可证得AD∥OC;
②连接DE、BE;上面已证得![]() =
=![]() ,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
③根据圆周角定理得到,GF⊥BE.又由②知,BE是∠CBD的平分线,根据等腰三角形的“三合一”性质得到EG=EF.故③正确;
④若FE=FC,则∠OCB=∠CEF=∠OEA=∠OAE,在Rt△OBC中,BD⊥OC,易得∠DBA=∠OCB(因为OC⊥BD),即∠DBA=∠EAB;因此![]() =
=![]() ,而这个条件并不一定成立.故④不正确.
,而这个条件并不一定成立.故④不正确.
①连接OD,DE,EB,CD,与BC是O的切线,易证△CDO≌△CBO,则∠DCO=∠BCO.故OC⊥BD.∵AB是直径,∴AD⊥BD,∴AD∥OC,故①正确;②∵CD是O的切线,∴∠CDE=12∠DOE,而∠BDE=12∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,因此E为△CBD的内心,故②正确;③如图,∵AB是直径,∴∠AEB=90,即GF⊥BE.又由②知,BE是∠CBD的平分线,∴BE是等腰△GBF的边GF上的中垂线,则EG=EF.故③正确;④若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,∴![]() =
=![]() ,而
,而![]() 和
和![]() 不一定相等,故④不正确.故选C.
不一定相等,故④不正确.故选C.

练习册系列答案
相关题目