题目内容
【题目】已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且 ![]() .
.
(1)求抛物线的方程;
(2)如图所示,过F的直线l与抛物线相交于A,D两点,与圆x2+(y﹣1)2=1相交于B,C两点(A,B两点相邻),过A,D两点分别作我校的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
【答案】
(1)
解:由题意可知P(4,0),Q(4, ![]() ),丨QF丨=
),丨QF丨= ![]() +
+ ![]() ,
,
由 ![]() ,则
,则 ![]() +
+ ![]() =
= ![]() ×
× ![]() ,解得:p=2,
,解得:p=2,
∴抛物线x2=4y
(2)
解:设l:y=kx+1,A(x1,y1),B(x2,y2),
联立 ![]() ,整理得:x2﹣4kx﹣4=0,
,整理得:x2﹣4kx﹣4=0,
则x1x2=﹣4,
由y= ![]() x2,求导y′=
x2,求导y′= ![]() ,
,
直线MA:y﹣ ![]() =
= ![]() (x﹣x1),即y=
(x﹣x1),即y= ![]() x﹣
x﹣ ![]() ,
,
同理求得MD:y= ![]() x﹣
x﹣ ![]() ,
,
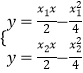 ,解得:
,解得: ![]() ,则M(2k,﹣1),
,则M(2k,﹣1),
∴M到l的距离d= ![]() =2
=2 ![]() ,
,
∴△ABM与△CDM的面积之积S△ABMS△CDM= ![]() 丨AB丨丨CD丨d2,
丨AB丨丨CD丨d2,
= ![]() (丨AF丨﹣1)(丨DF丨﹣1)d2,
(丨AF丨﹣1)(丨DF丨﹣1)d2,
= ![]() y1y2d2
y1y2d2![]()
![]() ×d2,
×d2,
=1+k2≥1,
当且仅当k=0时取等号,
当k=0时,△ABM与△CDM的面积之积的最小值1
【解析】(1)求得P和Q点坐标,求得丨QF丨,由题意可知, ![]() +
+ ![]() =
= ![]() ×
× ![]() 即可求得p的值,求得椭圆方程;(2)设直线方程,代入抛物线方程,由韦达定理x1x2=﹣4,求导,根据导数的几何意义,求得切线方程,联立求得M点坐标,根据点到直线距离公式,求得M到l的距离,利用三角形的面积公式,即可求得△ABM与△CDM的面积之积的最小值.
即可求得p的值,求得椭圆方程;(2)设直线方程,代入抛物线方程,由韦达定理x1x2=﹣4,求导,根据导数的几何意义,求得切线方程,联立求得M点坐标,根据点到直线距离公式,求得M到l的距离,利用三角形的面积公式,即可求得△ABM与△CDM的面积之积的最小值.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目