题目内容
如图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分;图2是车棚顶部截面的示意图.
(1)用尺规在图2中作出弧AB所在圆的圆心(保留作图痕迹,不写作法与证明);
(2)车棚顶部是用一种帆布覆盖的,由图1中给出数据求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留π).

(1)用尺规在图2中作出弧AB所在圆的圆心(保留作图痕迹,不写作法与证明);
(2)车棚顶部是用一种帆布覆盖的,由图1中给出数据求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留π).

(1)如图所示:
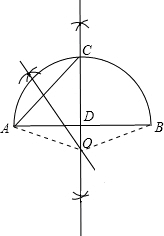 ;
;
(2)如(1)中的图,根据垂径定理,得AD=2
.
设圆的半径是r.
在直角三角形AOD中,根据勾股定理,得
r2=(r-2)2+(2
)2,
解得r=4.
则OD=2.
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
则弧AB的长是
=
,
则覆盖棚顶的帆布的面积是
×60=160π(m2).
 ;
;(2)如(1)中的图,根据垂径定理,得AD=2
| 3 |
设圆的半径是r.
在直角三角形AOD中,根据勾股定理,得
r2=(r-2)2+(2
| 3 |
解得r=4.
则OD=2.
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
则弧AB的长是
| 120π×4 |
| 180 |
| 8π |
| 3 |
则覆盖棚顶的帆布的面积是
| 8π |
| 3 |

练习册系列答案
相关题目






