��Ŀ����
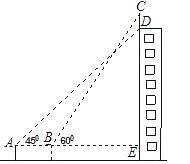
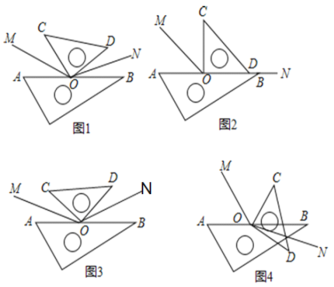
����Ŀ���ۺ���̽�����ⱳ����ѧ����ϣ���ʦ��һ�����dz߰�ͼ��1����ʾλ�ðڷţ��ֱ�������AOC����BOD��ƽ����OM��ON��Ȼ������������⣺�����MON�Ķ�����
����̽������ȤС�顱��ͬѧ��������������̽����ʦ��������⣬���ǽ����dz߷ֱ�ͼ2��ͼ3��ʾ�ķ�ʽ�ڷţ�OM��ON��Ȼ�ǡ�AOC�͡�BOD�Ľ�ƽ���ߣ����У���ͼ2��ʽ�ڷ�ʱ�����Կ�����ON��OD��OB��ͬһֱ���ϣ���ͼ3��ʽ�ڷ�ʱ����AOC�͡�BOD��ȣ�
��1�������������ȤС�顱���м��㣺ͼ2�С�MON�Ķ���Ϊ�� ���㣮ͼ3�С�MON�Ķ���Ϊ�� ���㣮
���ָ���
�����ͼ2��ͼ3��ʾ�������ȤС�顱�ֶ�ͼ1��ʾ������������ۣ�
С��������ͼ1�С�AOC�͡�BOD�ĺ�Ϊ90�㣬�����������õ���MOC�͡�NOD�ĺͣ��������������MON�Ķ�����
С�������BODΪx�㣬���Ǿ����ú�x��ʽ�ӷֱ��ʾ����NOD�͡�MOC����������Ҳ�������MON�Ķ�����
��2������������ǵ�̸�����ݣ����ͼ1�С�MON�Ķ�����
�����չ
�ܵ�����ȤС�顱�����������ǻ�С�顱�����dz߰�ͼ4��ʾ��ʽ�ڷţ��ֱ�������AOC����BOD��ƽ����OM��ON��������ΪҲ�������MON�Ķ�����
��3����ͬ�⡰�ǻ�С�顱�Ŀ�������ͬ�⣬�����MON�Ķ���������ͬ�⣬��˵�����ɣ�
���𰸡���1��135��135����2����MON��135�㣻��3��ͬ�⣬��MON����90�㩁![]() x�㣩+x��+��45�㩁
x�㣩+x��+��45�㩁![]() x�㣩��135��.
x�㣩��135��.
��������
��1��������ɵã���MON��![]() ��90��+90�㣬��MON��
��90��+90�㣬��MON��![]() ��AOC+
��AOC+![]() ��BOD+��COD�����ɵó��𰸣�
��BOD+��COD�����ɵó��𰸣�
��2�����ݡ�OM��ON�ǡ�AOC�͡�BOD�Ľ�ƽ���ߡ��������MOC+��NOD���֡�MON������MOC+��NOD��+��COD�����ɵó��𰸣�
��3�����BOC��x�㣬���AOC��180�㩁x�㣬��BOD��90�㩁x�㣬���������MOC�͡�BON���֡�MON����MOC+��BOC+��BON�����ɵó���.
�⣺��1��ͼ2�С�MON��![]() ��90��+90�㣽135�㣻ͼ3�С�MON��
��90��+90�㣽135�㣻ͼ3�С�MON��![]() ��AOC+
��AOC+![]() ��BOD+��COD��
��BOD+��COD��![]() ����AOC+��BOD��+90�㣽
����AOC+��BOD��+90�㣽![]() 90��+90�㣽135�㣻
90��+90�㣽135�㣻
�ʴ�Ϊ��135��135��
��2���ߡ�COD��90�㣬
���AOC+��BOD��180�㩁��COD��90�㣬
��OM��ON�ǡ�AOC�͡�BOD�Ľ�ƽ���ߣ�
���MOC+��NOD��![]() ��AOC+
��AOC+![]() ��BOD��
��BOD��![]() ����AOC+��BOD����45�㣬
����AOC+��BOD����45�㣬
���MON������MOC+��NOD��+��COD��45��+90�㣽135�㣻
��3��ͬ�⣬
���BOC��x�㣬���AOC��180�㩁x�㣬��BOD��90�㩁x�㣬
��OM��ON�ǡ�AOC�͡�BOD�Ľ�ƽ���ߣ�
���MOC��![]() ��AOC��
��AOC��![]() ��180�㩁x�㣩��90�㩁
��180�㩁x�㣩��90�㩁![]() x�㣬
x�㣬
��BON��![]() ��BOD��
��BOD��![]() ��90�㩁x�㣩��45�㩁
��90�㩁x�㣩��45�㩁![]() x�㣬
x�㣬
���MON����MOC+��BOC+��BON����90�㩁![]() x�㣩+x��+��45�㩁
x�㣩+x��+��45�㩁![]() x�㣩��135�㣮
x�㣩��135�㣮

����Ŀ��ij������2014��1���𣬾���������ˮ��ʼʵ�н���ʽ����ˮ�ۣ��ý���ʽ����ˮ�۷�Ϊ���������±���ʾ����
����ˮ�����֣� | ˮ�ۣ�Ԫ/�֣� |
��һ�� 20�����£���20�֣� | 1��6 |
�ڶ��� 20����30�֣���30�֣� | 2��4 |
������ 30������ | 3��2 |
����ij�û�������ˮ��Ϊ32�֣�����������Ӧ��ˮ��Ϊ��
1��6��20��2��4��10��3��2��2��62��4��Ԫ��
��1��������û�������ˮ��Ϊ12�֣������ɵ�ˮ��Ϊ Ԫ��
��2��������û��ɵ�ˮ��Ϊ39��2Ԫ����������ˮ�� �֣�
��3��������û�������ˮ��Ϊa�֣�����û�����Ӧ��ˮ�Ѷ���Ԫ�����ú�a�Ĵ���ʽ��ʾ��������