Question

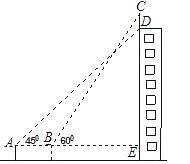
【题目】如图，某幢大楼顶部有一块广告牌CD，甲、乙两人分别在A、B两处，甲测得点D的仰角为45°，乙测得点C的仰角为60°，已知两人使用的测角仪的高度AF、BG相等，且A、B、E三点在一条直线上，AB=8m，BE=15m．求广告牌CD的高（精确到1m）．

Answer 1

【答案】3m．

【解析】试题分析：在Rt△ADE和Rt△BCE中，分别求出CE和DE的长度，然后可求得CD=CE﹣DE．

试题解析：解：∵AB=8m，BE=15m，∴AE=AB+BE=23m．在Rt△ADE中，∵∠DAE=45°，∴DE=AE=23m．在Rt△CBE中，∵∠CBE=60°，BE=15m，∴CE=BEtan60°=15m，则CD=CE﹣DE=15﹣23≈3（m）．

答：广告牌CD的高为3m．