题目内容
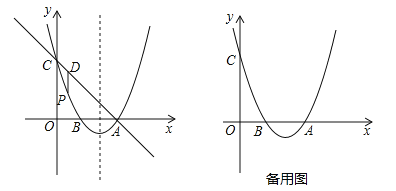
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 第一象限内的图象相交于点
第一象限内的图象相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)观察反比例函数![]() 的图象,当
的图象,当![]() 时,请直接写出
时,请直接写出![]() 的取值范围;
的取值范围;
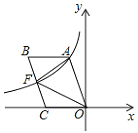
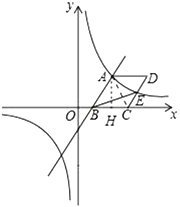
(3)如图,以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,双曲线交
在第一象限,双曲线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() .
.

【答案】(1)n=3,k=12;(2)![]() 或
或![]() ;(3)S△ABE=
;(3)S△ABE=![]() .
.
【解析】
(1)把A点坐标代入一次函数解析式可求得n,则可求得A点坐标,代入反比例函数解析式则可求得k的值;
(2)根据反比例函数的性质,可得答案;
(3)根据自变量与函数值的对应关系,可得B点坐标,根据两点间距离公式,可得AB,根据根据菱形的性质,可得BC的长,根据平行线间的距离相等,可得S△ABE=S△ABC.
解:(1)把![]() 点坐标代入一次函数解析式可得
点坐标代入一次函数解析式可得
![]() ,
,
∴![]() ,
,
∵![]() 点在反比例函数图象上,
点在反比例函数图象上,
∴![]() ;
;
(2)由图象,得
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
(3)过![]() 点作
点作![]() 垂足为
垂足为![]() ,连接
,连接![]()
 ,
,
∵一次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∴![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】一辆出租车从![]() 地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(
地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(![]() ,单位:
,单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 |
|
|
|
|
(1)写出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶多少路程?