题目内容
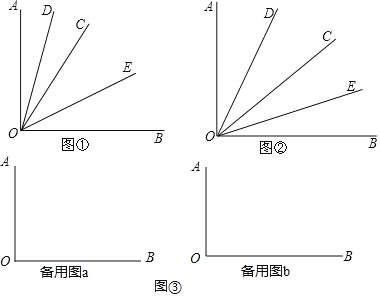
【题目】某旅游景点的年游客量y（万人）是门票价格x（元）的一次函数，其函数图像如下图．
（1）求y关于x的函数解析式；
（2）经过景点工作人员统计发现：每卖出一张门票所需成本为20元．那么要想获得年利润11500万元，且门票价格不得高于230元，该年的门票价格应该定为多少元？
【答案】（1）y=-x+300（2）70
【解析】试题分析：
（1）设y与x的函数关系式为：y=kx+b，代入图中两点的坐标，列出方程组，解方程组求得k、b的值，即可得到所求的解析式；
（2）设门票价格定为x元，结合（1）可列出方程（x-20）(-x+300)=11500，解方程即可.
试题解析：
（1）设
，函数图像过点（200,100）， （50,250）
代入解析式得： 
，解得： 
，
∴y关于x的解析式为： 
；
（2）设门票价格定为x元，依题意可得：
，
整理得： 
， 解之得：x=70或者x=250（舍去），
答：门票价格应该定为70元.
练习册系列答案
相关题目
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
