题目内容
【题目】如图,已知AB∥CD,∠BCD的三等分线是CP,CQ,又CR⊥CP,若∠B=78°,则∠RCE=( ) 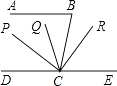
A.66°
B.65°
C.58°
D.56°
【答案】D
【解析】解:∵AB∥CD,∠B=78°, ∴∠BCD=180°﹣78°=102°,
∵∠BCD的三等分线是CP,CQ,
∴∠BCP= ![]() ×∠BCD=
×∠BCD= ![]() ×102°=68°,
×102°=68°,
∵CR⊥CP,
∴∠BCR=90°﹣∠BCP=90°﹣68°=22°,
∵AB∥CD,∠B=78°,
∴∠BCE=∠B=78°,
∴∠RCE=∠BCE﹣∠BCR=78°﹣22°=56°.
故选D.
【考点精析】掌握角的运算和平行线的性质是解答本题的根本,需要知道角之间可以进行加减运算;一个角可以用其他角的和或差来表示;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目