题目内容
【题目】如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
(1)求证:BD=CE;
(2)若BE、CD交于点F,求证:△BDF≌△CEF;
(3)在(2)的条件下连接AF,求证:AF平分∠BAC.

【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)要证BD=CE只要证明AD=AE即可,而证明△ABE≌△ACD,则可得AD=AE.
(2)由BD=CE,∠B=∠C,∠DFB=∠EFC,易证△BDF≌△CEF;
(3)要证AF平分∠BAC,只要证△ABF≌△ACF即可.
证明:(1)在△ABE和△ACD中,
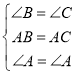 ,
,
∴△ABE≌△ACD(ASA),
∴AD=AE,
∵AB=AC,
∴BD=CE;
(2)在△BDF和△CEF中,
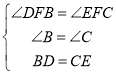 ,
,
∴△BDF≌△CEF(AAS);
(3)连接AF,如图,
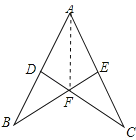
∵△BDF≌△CEF,
∴BF=CF,
在△ABF和△ACF中,
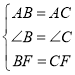 ,
,
∴△ABF≌△ACF(SAS),
∴∠BAF=∠CAF,
∴AF平分∠BAC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目