Question

【题目】如图，在ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．

（1）求证：四边形ABEF是菱形；
（2）若AB=4，AD=6，∠ABC=60°，求tan∠ADP的值．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC．

∴∠DAE=∠AEB．

∵AE是角平分线，

∴∠DAE=∠BAE．

∴∠BAE=∠AEB．

∴AB=BE．

同理AB=AF．

∴AF=BE．

∴四边形ABEF是平行四边形．

∵AB=BE，

∴四边形ABEF是菱形．

（2）解：作PH⊥AD于H，

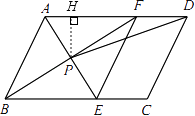
∵四边形ABEF是菱形，∠ABC=60°，AB=4，

∴AB=AF=4，∠ABF=∠AFB=30°，AP⊥BF，

∴AP= AB=2，

∴PH= ，DH=5，

∴tan∠ADP= = ．

【解析】（1）根据平行四边形的性质及角平分线的定义先证明出四边形ABEF是平行四边形．再根据一组邻边相等得平行四边形是菱形得出结论；（2）作PH⊥AD于H，根据菱形的性质得出AB=AF=4，∠ABF=∠AFB=30°，AP⊥BF，从而得出PH，DH的长度，根据正切函数的定义得出结论。