Question

【题目】在 中，，．将线段绕着点逆时针旋转得到线段，旋转角为，且，连接、．

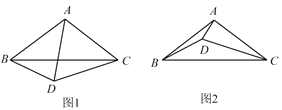
（1）如图 1，当时，的大小为 　 ；

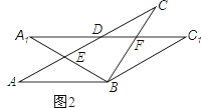
（2）如图 2，当时，的大小为 　 ；

（提示：可以作点D关于直线BC的对称点）

（3）当为 　 ° 时，可使得的大小与（1）中的结果相等．

Answer 1

【答案】（1） ；（2） ；（3），，或，．

【解析】

(1)由∠BAC=100，AB=AC，可以确定∠ABC=∠ACB=40，旋转角为α，α=60°时△ACD是等边三角形，且AC=AD=AB=CD，知道∠BAD的度数，进而求得∠CBD的大小；

(2) 作点D关于直线BC的对称点D/，连接A D/、B D/、C D/，根据旋转和对称的性质即可得；

(3)结合(1)(2)的解题过程可以发现规律，△ACD是等边三角形时，CD在△ABC内部时，CD在△ABC外部时，求得答案.

解：(1)∵∠BAC=100，AB=AC，

∴∠ABC=∠ACB=40，当α=60时，

由旋转的性质得AC=CD，

∴△ACD是等边三角形，

∴∠DAC=60，

∴∠BAD=∠BAC∠DAC=10060=40，

∵AB=AC，AD=AC，

∴AB=AD，

∴∠ABD=∠ADB=(180∠BAD)=70，

∴∠CBD=∠ABD∠ABC=7040=30；

(2)如图，作点D关于直线BC的对称点D/，连接A D/、B D/、C D/，

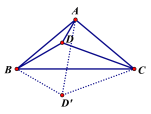
∵∠BAC=100，AB=AC，

∴∠ABC=∠ACB=40，当α=20时，

∴∠BCD=20，

由旋转和对称的性质可知，∠BCD/=∠BCD=20，AC=CD=CD/，

∴△ACD/是等边三角形，

由(1)可知∠CBD/=30，

∴∠CBD=∠CBD/=30；

(3)①由(1)可知，∠α=60时可得∠CBD=30；

②由(2)可知，∠α=20时可得∠CBD=30；

③在图1中以C为圆心CD为半径画圆弧交BD的延长线于点D1，连接CD1，

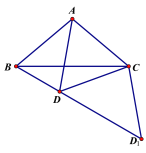
∵∠CDD1=∠CBD+∠BCD=30+=50，

∴∠DCD1=1802∠CDD1=180100=80，

∴∠α=60+∠DCD1=140；

④在图2中以C为圆心CD为半径画圆弧交BD的延长线于点D2，连接CD2，

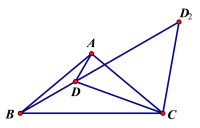
∵∠CDD2=∠CBD+∠BCD=30+=50，

∴∠DCD2=1802∠CDD2=180100=80，

∴∠ACD2=∠DCD2-∠ACD=80-20=60，

∴∠α=360-60=300.

综上所述,α为20、60、140、300时，∠CBD=30.

故答案为：（1） ；（2） ；（3），，或，．