题目内容
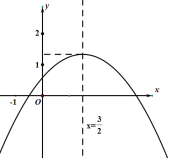
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
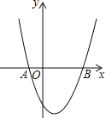
【答案】(1)y=x2-2x-3,(1,-4)(2)(-2,3)(4,3)
【解析】
(1)把A、B两点坐标代入抛物线解析式,利用待定系数法可求得其解析式,再化为顶点式即可求得其顶点坐标;
(2)设P(x,y),根据三角形的面积公式以及S△PAB=10,即可算出y的值,代入抛物线解析式即可得出点P的坐标.
(1)∵抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4);
(2)∵A(-1,0)、B(3,0),
∴AB=4.
设P(x,y),则S△PAB=![]() AB|y|=2|y|=10,
AB|y|=2|y|=10,
∴|y|=5,
∴y=±5.
①当y=5时,x2-2x-3=5,解得:x1=-2,x2=4,
此时P点坐标为(-2,5)或(4,5);
②当y=-5时,x2-2x-3=-5,方程无解;
综上所述,P点坐标为(-2,5)或(4,5).

 应用题作业本系列答案
应用题作业本系列答案【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)