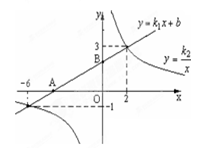
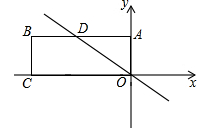
题目内容
如图,已知反比例函数 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, ),
),

(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, ),
),
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
(1)反比例函数的表达式为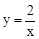 ,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.
,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.
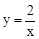 ,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.
,一次函数的表达式为y=x+1;(2)x<-2或0<x<1.试题分析:(1)把A(1,
 )代入解析式
)代入解析式 ,即可求出k的值;把求出的A点坐标代入一次函数y=x+b的解析式,即可求出b的值;从而求出这两个函数的表达式;
,即可求出k的值;把求出的A点坐标代入一次函数y=x+b的解析式,即可求出b的值;从而求出这两个函数的表达式;(2)将两个函数的解析式组成方程组,其解即为另一点的坐标.当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围.
试题解析:(1)∵已知反比例函数
 经过点A(1,
经过点A(1, ),
),∴
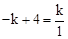 ,解得∴k="2." ∴A(1,2).
,解得∴k="2." ∴A(1,2).∵一次函数y=x+b的图象经过点A(1,2),∴2=1+b,解得b=1.
∴反比例函数的表达式为
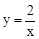 ,一次函数的表达式为y=x+1.
,一次函数的表达式为y=x+1.(2)由
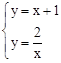 消去y,得
消去y,得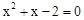 ,即
,即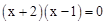 ,∴x=-2或x=1.∴y=-1或y=2.
,∴x=-2或x=1.∴y=-1或y=2.∴
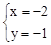 或
或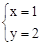
∵点B在第三象限,∴点B的坐标为
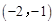 .
.由图象可知,当反比例函数的值大于一次函数的值时,x的取值范围是x<-2或0<x<1.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 的取值范围是
的取值范围是 时,函数值
时,函数值 的取值范围是
的取值范围是 ,那么此函数的解析式是( )
,那么此函数的解析式是( )

 或
或
 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.

 时所用的时间.
时所用的时间. 是一次函数,则k= .
是一次函数,则k= . ,当
,当 的值由
的值由 增加到2时,该线段运动所经过的平面区域的面积为( )
增加到2时,该线段运动所经过的平面区域的面积为( ) 和反比例函数
和反比例函数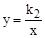 的图像,判断下列结论正确的个数有( )
的图像,判断下列结论正确的个数有( )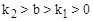 ;②直线
;②直线 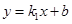 与坐标轴围成的△ABO的面积是4;③方程组
与坐标轴围成的△ABO的面积是4;③方程组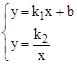 的解为,
的解为,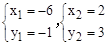 ;④当-6<x<2时,有
;④当-6<x<2时,有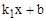 >
>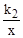 .
.