题目内容
【题目】已知,![]() 内接于
内接于![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() .
.
(1)如图,求证:![]() ;
;
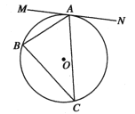
(2)如图,点![]() 为
为![]() 的中点,射线
的中点,射线![]() 交
交![]() 于点
于点![]() ,交优弧
,交优弧![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
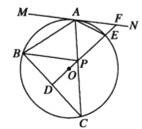
【答案】(1)见解析;(2)见解析;(3)![]() 的半径为
的半径为![]()
【解析】
(1)如下图,根据切线和直径所对圆周角为90°得到![]() 和
和![]() ,通过角度转化可证
,通过角度转化可证![]() ;
;
(2)如下图,设![]() ,推导可得出
,推导可得出![]() ,
,![]() ,
,![]() ,从而证
,从而证![]() ;
;
(3)如下图,设![]() ,则
,则![]() ,先证
,先证![]() ,从而得出
,从而得出![]() ,最后可利用
,最后可利用![]() 的关系得出k的值和
的关系得出k的值和![]() 的半径.
的半径.
(1)证明:过点![]() 作直径
作直径![]() ,连接
,连接![]() .
.
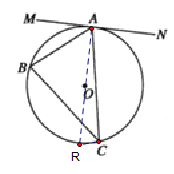
∵![]() 是
是![]() 直径,∴
直径,∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .
.
∵![]() 是
是![]() 切线,∴
切线,∴![]() .
.
∴![]() .∴
.∴![]() .
.
(2)证明:延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,

设![]() .∵
.∵![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() .
.
∵点![]() 为
为![]() 中点,
中点,![]() 不是直径,
不是直径,
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴AG∥BC.∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]() .
.
(3)解:如图,连接![]() ,设
,设![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
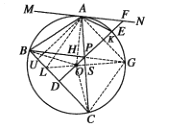
由(2)知![]() 于点
于点![]() ,且
,且![]() ,
,
∴![]() .
.
∵BP∥MN,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 垂直平分
垂直平分![]() .∴
.∴![]() .
.
∴![]() .
.
∴设![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() ,
,![]() .
.
∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 垂直平分
垂直平分![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() 垂直平分
垂直平分![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴![]() ,即
,即![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目