题目内容
【题目】在平面直角坐标系中,若要把一条直线平移到某个位置,经常可通过方式一:上(下)平移,或者方式二:左(右)平移的其中一种达到目的.现有直线![]() 交
交![]() 轴于点
轴于点![]() ,若把直线
,若把直线![]() 向右平移8个单位长度得到直线
向右平移8个单位长度得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的解析式,并说明直线
的解析式,并说明直线![]() 若按方式一是如何平移到直线
若按方式一是如何平移到直线![]() 的位置;
的位置;
(2)若直线![]() 上的一点
上的一点![]() ,点
,点![]() 按方式一平移后在直线
按方式一平移后在直线![]() 上的对应点记为点
上的对应点记为点![]() .
.
①若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示) ;
的式子表示) ;
②当![]() 时,试证明直线
时,试证明直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.

【答案】(1)![]() ,向上平移4个单位;(2)①点
,向上平移4个单位;(2)①点![]() 的坐标为
的坐标为![]() ;②证明见解析
;②证明见解析
【解析】
(1)根据直线平行k相等,可求直线![]() 的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线
的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线![]() 的;
的;
(2)①根据B在直线![]() 上可得
上可得![]() ,由B的对应点为C,可得点C
,由B的对应点为C,可得点C![]() ,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是
,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是![]() ,设点P的横坐标为
,设点P的横坐标为![]() ,代入可得结论;
,代入可得结论;
②证明四边形ABCD是平行四边形,连接BD、AC,交点记为点E,确定E![]() ,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线
,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线![]() 必过E点,可得结论.
必过E点,可得结论.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,
∴直线![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() ,
,
按方式二平移后的对应点为![]() ,且在直线
,且在直线![]() 上,
上,
设直线![]() 的解析式为
的解析式为![]()
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
∴直线![]() 若按方式一向上平移4个单位得到直线
若按方式一向上平移4个单位得到直线![]() ;
;
(2)①如图1,∵点![]() 在直线
在直线![]() 上,
上,
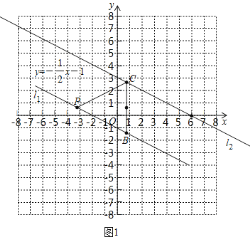
![]() ,
,
∴点![]() ,
,
由(1)得,点![]() ,且
,且![]() 轴,
轴,
∴![]() 的中点坐标为
的中点坐标为![]() ,
,
![]()
∴点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
又∵![]() 轴,
轴,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
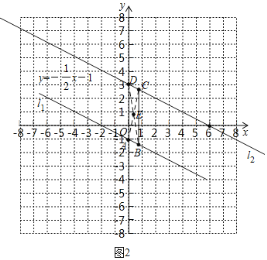
②如图2,根据题意得:![]() ,
,![]() ,
,![]()
![]() ,
,
由平移可知![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
连接四边形![]() 的对角线,交点记为点
的对角线,交点记为点![]() ,则
,则![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]()
![]() 过点
过点![]() 的直线把平行四边形
的直线把平行四边形![]() 的面积二等分,
的面积二等分,
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
即当![]() 时,直线
时,直线![]() 必过
必过![]() 点,
点,
直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案