题目内容
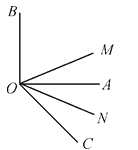
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.

【答案】解:(1)54°;(2)120°
【解析】试题分析:(1)由对顶角相等可得∠AOC=∠BOD=36°,由∠COE=90°可得∠EOD=90°,所以∠BOE=∠EOD-∠BOD=54°;(2)由∠COE:∠EOB:∠BOD=4:3:2,可得∠EOB=180°×![]() =60°,所以∠AOE=180°-∠EOB=120°.
=60°,所以∠AOE=180°-∠EOB=120°.
试题解析:
解:(1)∵∠AOC=36°,∠COE=90°,
∴∠BOD=36°,∠EOD=90°,
∴∠BOE=90-36°=54°;
(2)∠COE:∠EOB:∠BOD=4:3:2,
∴∠EOB=180°×![]() =60°,
=60°,
∴∠AOE=180°-∠EOB=180°-60°=120°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目