ЬтФПФкШн
ЁОЬтФПЁПФГаЁЧјЮЊСЫТЬЛЏЛЗОГЃЌМЦЛЎЗжСНДЮЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНј
СНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВн
СНжжЛЈВн![]() ПУКЭ
ПУКЭ![]() ПУЃЌЙВЛЈЗб
ПУЃЌЙВЛЈЗб![]() дЊЃЛЕкЖўДЮЗжБ№ЙКНј
дЊЃЛЕкЖўДЮЗжБ№ЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВн
СНжжЛЈВн![]() ПУКЭ
ПУКЭ![]() ПУЃЎСНДЮЙВЛЈЗб
ПУЃЎСНДЮЙВЛЈЗб![]() дЊЃЈСНДЮЙКНјЕФ
дЊЃЈСНДЮЙКНјЕФ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
СНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
ЃЈ![]() ЃЉ
ЃЉ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
СНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ![]() ЃЉШєЙКТђ
ЃЉШєЙКТђ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнЙВ
СНжжЛЈВнЙВ![]() ПУЃЌЧв
ПУЃЌЧв![]() жжЛЈВнЕФЪ§СПЩйгк
жжЛЈВнЕФЪ§СПЩйгк![]() жжЛЈВнЕФЪ§СПЕФ
жжЛЈВнЕФЪ§СПЕФ![]() БЖЃЌЧыФуИјГівЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
БЖЃЌЧыФуИјГівЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
ЁОД№АИЁПЃЈ![]() ЃЉAЃЌBСНжжЛЈВнМлИёЗжБ№ЮЊ20дЊКЭ5дЊЃЛ
ЃЉAЃЌBСНжжЛЈВнМлИёЗжБ№ЮЊ20дЊКЭ5дЊЃЛ
ЃЈ![]() ЃЉЗбгУзюЪЁЕФЗНАИЮЊЙКТђAжжЛЈВн11ПУЃЌЙКТђBжжЛЈВн20ПУЃЌЛЈЗбзюЩйЮЊ320дЊЃЎ
ЃЉЗбгУзюЪЁЕФЗНАИЮЊЙКТђAжжЛЈВн11ПУЃЌЙКТђBжжЛЈВн20ПУЃЌЛЈЗбзюЩйЮЊ320дЊЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшAжжЛЈВнУППУЕФМлИёxдЊЃЌBжжЛЈВнУППУЕФМлИёyдЊЃЌИљОнЕквЛДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн30ПУКЭ15ПУЃЌЙВЛЈЗб940дЊЃЛЕкЖўДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн12ПУКЭ5ПУЃЌСНДЮЙВЛЈЗб675дЊЃЛСаГіЗНГЬзщЃЌМДПЩНтД№ЃЎЃЈ2ЃЉЩшAжжЛЈВнЕФЪ§СПЮЊmжъЃЌдђBжжЛЈВнЕФЪ§СПЮЊЃЈ31-mЃЉжъЃЌИљОнBжжЛЈВнЕФЪ§СПЩйгкAжжЛЈВнЕФЪ§СПЕФ2БЖЃЌЕУГіmЕФЗЖЮЇЃЌЩшзмЗбгУЮЊWдЊЃЌИљОнзмЗбгУ=СНжжЛЈВнЕФЗбгУжЎКЭНЈСЂКЏЪ§ЙиЯЕЪНЃЌгЩвЛДЮКЏЪ§ЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ![]() ЃЉЩш
ЃЉЩш![]() ЃЌ
ЃЌ ![]() СНжжЛЈВнУППУЕФМлИёЗжБ№ЮЊ
СНжжЛЈВнУППУЕФМлИёЗжБ№ЮЊ![]() дЊКЭ
дЊКЭ![]() дЊЃЎ
дЊЃЎ
гЩЬтвтЕУ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ
Д№ЃК ![]() ЃЌ
ЃЌ ![]() СНжжЛЈВнМлИёЗжБ№ЮЊ
СНжжЛЈВнМлИёЗжБ№ЮЊ![]() дЊКЭ
дЊКЭ![]() дЊЃЎ
дЊЃЎ
ЃЈ![]() ЃЉЩшЙКТђ
ЃЉЩшЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌдђЙКТђ
ПУЃЌдђЙКТђ![]() жжЛЈВнЮЊ
жжЛЈВнЮЊ![]() ПУЃЌ
ПУЃЌ
гЩЬтвтЕУ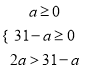 ЃЌЧв
ЃЌЧв![]() ЮЊећЪ§ЃЌ
ЮЊећЪ§ЃЌ
НтЕУЃК ![]() Чв
Чв![]() ЮЊећЪ§ЃЌ
ЮЊећЪ§ЃЌ
гЩЃЈ![]() ЃЉПЩжЊЃЌ
ЃЉПЩжЊЃЌ ![]() ЕФМлИёЮЊ
ЕФМлИёЮЊ![]() дЊ/ПУЃЌ
дЊ/ПУЃЌ ![]() ЕФМлИёЮЊ
ЕФМлИёЮЊ![]() дЊ/ПУЃЌ
дЊ/ПУЃЌ
ЩшЗбгУЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
гЩвЛДЮКЏЪ§ЕФаджЪПЩЕУЃК ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЁрЕБ![]() ШЁзюаЁећЪ§
ШЁзюаЁећЪ§![]() ЪБЃЌзюаЁжЕЮЊЃК
ЪБЃЌзюаЁжЕЮЊЃК ![]() ЃЌ
ЃЌ
Д№ЃКЗбгУзюЪЁЕФЗНАИЮЊЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌЙКТђ
ПУЃЌЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌЛЈЗбзюЩйЮЊ
ПУЃЌЛЈЗбзюЩйЮЊ![]() дЊЃЎ
дЊЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ