Question

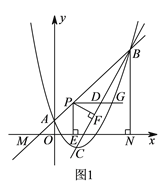
【题目】如图，抛物线y=x2+bx+c与x轴相交于A、B两点，点B的坐标为（3，0），与y轴相交于点C（0，﹣3），顶点为D．

（1）求出抛物线y=x2+bx+c的表达式；

（2）连结BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m．

①当m为何值时，四边形PEDF为平行四边形．

②设四边形OBFC的面积为S，求S的最大值．

Answer 1

【答案】（1）y=x2﹣2x﹣3；（2）①2；②．

【解析】分析:（1）由B、C两点的坐标，利用待定系数法可求得抛物线的表达式；

（2）①可求得直线BC的解析式，则可表示出P、F的坐标，从而可表示出PF和DE的长，由平行四边形的性质可知PF=DE，则可得到关于m的方程，可求得m的值；②用m可表示出PF的长，则可表示出△BCF的面积，从而可表示出四边形OBFC的面积，利用二次函数的性质可求得其最大值．

本题解析:（1）∵抛物线过B、C两点，

∴，解得,

∴抛物线表达式为y=x2﹣2x﹣3；

（2）①∵B（3，0），C（0，﹣3），

∴直线BC解析式为y=x﹣3，

∵y=x2﹣2x﹣3=（x﹣1）2﹣4，

∴D（1，﹣4），

∴E（1，﹣2），

∴DE=﹣2﹣（﹣4）=2，

∵PF∥DE，且P（m，m﹣3），

∴F（m，m2﹣2m﹣3），

∵点P为线段BC上的一个动点，

∴PF=m﹣3﹣（m2﹣2m﹣3）=﹣m2+3m，

当四边形PEDF为平行四边形时，则有PF=DE=2，

即﹣m2+3m=2，解得m=1（舍去）或m=2，

∴当m的值为2时，四边形PEDF为平行四边形；

②由①可知PF=﹣m2+3m，

∴S△FBC=PFOB=×3（﹣m2+3m）=﹣（m﹣）2+，

∵S△OBC=OBOC=×3×3=，

∴S=S△FBC+S△OBC=﹣（m﹣）2++=﹣（m﹣）2+，

∵﹣＜0，

∴当m=时，S有最大值

点睛:本题考查了二次函数的应用,涉及待定系数法、平行四边形的性质、三角形的面积、二次函数的性质及方程思想等知识，本题考查知识点较多，综合性较强，难度适中.