题目内容
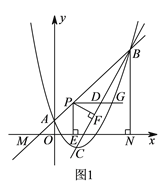
【题目】如图,已知⊙![]() 的半径为
的半径为![]() ,
, ![]() 为直径,
为直径, ![]() 为弦.
为弦. ![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿着
沿着![]() 翻折后,点
翻折后,点![]() 与圆心
与圆心![]() 重合,延长
重合,延长![]() 至
至![]() ,使
,使![]() ,链接
,链接![]() .
.
(![]() )求
)求![]() 的长.
的长.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )点
)点![]() 为
为![]() 的中点,在
的中点,在![]() 延长线上有一动点
延长线上有一动点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (
(![]() 与
与![]() 、
、![]() 不重合).则
不重合).则![]() 为一定值.请说明理由,并求出该定值.
为一定值.请说明理由,并求出该定值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得![]() ,从而得到GEGF=AG2,再根据等腰直角三角形的性质求解即可.
,从而得到GEGF=AG2,再根据等腰直角三角形的性质求解即可.
(![]() )连接
)连接![]() ,
,

∵![]() 沿
沿![]() 翻折后,
翻折后, ![]() 与
与![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )
)![]() ,
, ![]() 为定值,
为定值,
连接![]() ,
, ![]() ,
, ![]() ,
,

∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为直径,
为直径, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目