题目内容
【题目】如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF.
求证:DE=DF.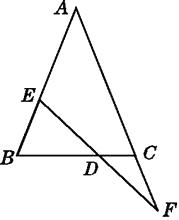
【答案】证明: 过点E作EG∥AC,交BC于点G ,  ,
,
∴∠F=∠DEG,∠ACB=∠EGB.
∵AB=AC,
∴∠ACB=∠B(等边对等角).
∴∠B=∠EGB.
∴BE=EG(等角对等边).
∵BE=CF,
∴EG=CF.
在△EGD和△FCD中,
∴△EGD≌△FCD(AAS).
∴DE=DF.
【解析】过点E作EG∥AC,交BC于点G , 根据二直线平行内错角,同位角相等得出∠F=∠DEG,∠ACB=∠EGB.根据等边对等角得出∠ACB=∠B,从而得出∠B=∠EGB.根据等角对等边得出BE=EG,从而得出EG=CF.然后利用AAS判断出△EGD≌△FCD,根据全等三角形对应边相等得出DE=DF。

练习册系列答案
相关题目