Question

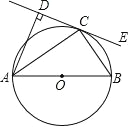
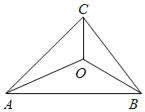
【题目】如图, △ABC中, AB=10, BC=8, AC=7, ⊙O为△ABC的内切圆, 切点分别是D, E, F. 求AD的长.

Answer 1

【答案】AD=4.5.

【解析】

连结OD、OF、 OA，根据切线的性质得到直角△AOD和直角△AOF，再根据直角三角形的判定HL证明全等，得到AD=AF，同理得到BD=BE, CE=CF，然后根据切线长定理求解即可.

解：连结OD, OF, OA.

∵AB, AC是⊙O的切线, ∴∠ODA=∠OFA=90°.

又∵OD=OF, OA=OA, ∴Rt△OAD≌Rt△OAF, ∴AD=AF.

同理, BD=BE, CE=CF.

∵BE+CE=BC=8, ∴BD+BE+CE+CF=16. ∴2AD=(10+8+7)-16=9, 即AD=4.5.