��Ŀ����
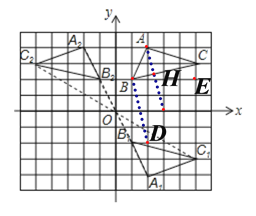
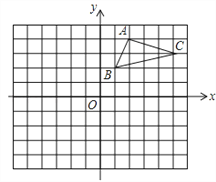
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��4��.
��1��������ABC����x��ԳƵ���A1B1C1����д����A1������A1 ________________��
��2��������A1B1C1��ԭ��O��ת180����õ�����A2B2C2����д����A2������A2__________________��
(3) ��ABC�Ƿ�Ϊֱ�������Σ���_________�����ǻ��߲��ǣ�.
��4�����ø��ͼ������BC���ϵĸ�AD�������AD�ij���AD=_____________.
���𰸡� ��2.-4�� ��-2,4�� ���� ![]()
�������������������1���ֱ��ҳ�A��B��C�������x��ĶԳƵ㣬��˳�����ӣ�Ȼ�����ͼ��д��A�����ꣻ
��2������A1B1C1�еĸ���A1��B1��C1��ԭ��O��ת180������A2B2C2����A1B1C1���ڵ�O�����ĶԳƣ��õ���Ӧ�Ķ�Ӧ��A2��B2��C2�����Ӹ���Ӧ�㼴����A2B2C2��
��3�����ݹ��ɶ����涨����ɣ�
��4������BD������A��AH��BD��BC���H��Ȼ�������������AH�ij��ȼ���.
�⣺��1����ͼ��ʾ����A1�����꣨2��-4����
��2����ͼ��ʾ����A2�����꣨-2��4����
��3����AC2=32+12=10, AB2=22+12=5, BC2=42+12=17,
��AC2+ AB2�� BC2,
����ABC����ֱ�������Σ�
��4������BD������A��AH��BD��BC���H.
��BB1=BE, ��BB1D=��BEC,B1D=CE,
���BB1D=��BEC,
���CBE=��DBB1.
�ߡ�DBE=��DBB1=90��,
���DBE=��CBE =90��,
��BD��BC,
��AH��BC.
��BC2=42+12=17,
��BC=![]() .
.
��S��ABC=4��2-![]() ��2��1-
��2��1-![]() ��3��1-
��3��1-![]() ��4��1=
��4��1=![]() ,
,
��![]() BC��AH=
BC��AH=![]() ,
,
��![]() AH=7,
AH=7,
��AH= ![]() .
.