题目内容
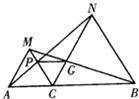 25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB.
25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB.分析:运用正三角形的特征:三边相等且三个角都是60°,证明△ACN≌△MCB,得∠ANC=∠MBC,再证△NPC≌△BGC,得PC=GC,
又∠PCG=60°,故△PCG为等边三角形,从而证得PG∥AB.
又∠PCG=60°,故△PCG为等边三角形,从而证得PG∥AB.
解答:证明:∵△ACM和△BCN为正三角形,
∴AC=MC,CN=CB,∠ACN=∠MCB.
∴△ACN≌△MCB.
∴∠ANC=∠MBC.
∵∠PCN=∠NCB=60°,
∴△NPC≌△BGC.
∴PC=GC.
又∵∠PCG=60°,
故△PCG为等边三角形.
∴∠PGC=∠GCB=60°.
∴PG∥AB.
∴AC=MC,CN=CB,∠ACN=∠MCB.
∴△ACN≌△MCB.
∴∠ANC=∠MBC.
∵∠PCN=∠NCB=60°,
∴△NPC≌△BGC.
∴PC=GC.
又∵∠PCG=60°,
故△PCG为等边三角形.
∴∠PGC=∠GCB=60°.
∴PG∥AB.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

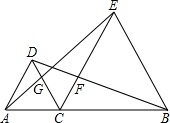 如图:已知点C在线段AB上,向AB的同侧分别作等边三角形△ACD、△CBE,连接AE交CD于G,连接BD交CE于F.
如图:已知点C在线段AB上,向AB的同侧分别作等边三角形△ACD、△CBE,连接AE交CD于G,连接BD交CE于F.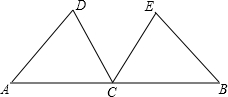 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE. 如图,已知点C在线段AB上,点M是AC的中点,点N在BC上,且CN:NB=1:2若AB=11cm,AC=5cm,求MN的值.
如图,已知点C在线段AB上,点M是AC的中点,点N在BC上,且CN:NB=1:2若AB=11cm,AC=5cm,求MN的值.