题目内容
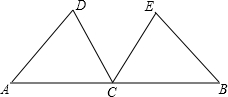如图：已知点C在线段AB的中点，点D、E在线段AB的同侧，AD∥CE，AD=CE．求证：DC∥EB．
分析：根据平行线性质得出∠A=∠ECB，求出AC=CB，根据SAS证△DAC≌△ECB，推出∠DCA=∠B，根据平行线的判定推出即可．
解答：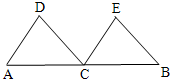
证明：∵AD∥CE，
∴∠A=∠ECB（两直线平行，同位角相等），
∵点C在线段AB的中点，
∴AC=CB，
在△DAC和△ECB中
，
∴△DAC≌△ECB（SAS），
∴∠DCA=∠B（全等三角形对应角相等），
∴DC∥EB（同位角相等，两直线平行）．
证明：∵AD∥CE，∴∠A=∠ECB（两直线平行，同位角相等），
∵点C在线段AB的中点，
∴AC=CB，
在△DAC和△ECB中
|
∴△DAC≌△ECB（SAS），
∴∠DCA=∠B（全等三角形对应角相等），
∴DC∥EB（同位角相等，两直线平行）．
点评：本题考查了全等三角形的性质和判定和平行线的性质和判定的应用．
练习册系列答案
相关题目
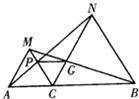25、如图，已知点C在线段AB上，以AC和BC为边在AB同侧作正△ACM和正△BCN，连接AN，BM，分别交CM，CN于点P，G，连接PG．求证：PG∥AB．
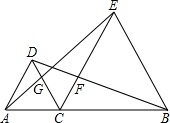如图：已知点C在线段AB上，向AB的同侧分别作等边三角形△ACD、△CBE，连接AE交CD于G，连接BD交CE于F．
如图，已知点C在线段AB上，点M是AC的中点，点N在BC上，且CN：NB=1：2若AB=11cm，AC=5cm，求MN的值．