��Ŀ����
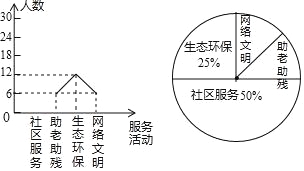
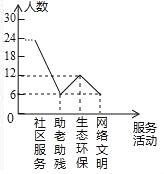
����Ŀ��Ϊ����������ס��Ѱ�����������������־Ը�����������������ˡ��������ҡ���־Ը���������Ӫ��ij��ѧ������ĩʱ�俪չ�ˡ��������С�����������̬�����������������ĸ�־Ը������ÿ��ֻ�μ�һ����������꼶ij��ȫ��ͬѧ���μ���־Ը���Ϊ�˽�־Ը�����������ռ��������ݺ������²�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1����������
��2���������ͳ��ͼ����������
��3��������ͳ��ͼ�У������������ֶ�Ӧ��Բ�ĽǵĶ�����
��4��С����С���μ���־Ը������������״ͼ���б���������Dzμ�ͬһ�����ĸ��ʣ�
���𰸡���1��48��2��ͼ�μ�������3��45����4��![]()
��������
�����������1�����ݲμ���̬�����������Լ��ٷֱȣ����ɽ�����⣻
��2�������������������������ͼ���ɣ�
��3������Բ�Ľ�=360�����ٷֱȣ����㼴�ɣ�
��4�����б������ɽ�����⣻
�����������1���ð�ȫ��������12��25%=48�ˣ�
��2��48��50%=24������ͳ����ͼ��ʾ��
��3��![]() ��360��=45�㣮
��360��=45�㣮
��4���ֱ��á�1��2��3��4���������������С�����������̬�����������������ĸ��������б����£�
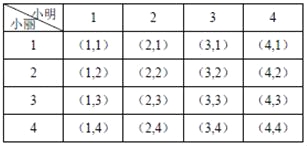
�����п�����16�֣��������Dzμ�ͬһ���4�֣�
�������Dzμ�ͬһ�����ĸ���P=![]() =
=![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�