题目内容
【题目】一个零件的形状如图,按规定∠A= 90°,∠B、∠C 分别是 32°和 21°.某检验工人量得∠BDC= 148°,就断定这个零件不合格,试用三角形的有关知识说明零件不合格的理由.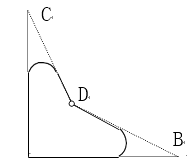
【答案】解:连接 AD 并延长至 E,假设是合格零件,
∴∠BDC=∠CDE+∠BDE,
=∠C+∠CAD+∠BAD+∠B,
=∠C+∠CAB+∠B,
又∵∠CAB= 90°,∠B=32°,∠C=21°,
∴∠BDC=21°+90°+32°=143°,
又∵检验工人现测得∠BDC=148°,
∴零件不合格.
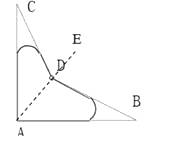
【解析】连接 AD 并延长至 E,假设是合格零件,由三角形的外角性质和已知条件得出∠BDC=∠CDE+∠BDE=143°,又由检验工人现测得∠BDC=148°,从而得出零件不合格.
【考点精析】利用三角形的外角对题目进行判断即可得到答案,需要熟知三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目