题目内容
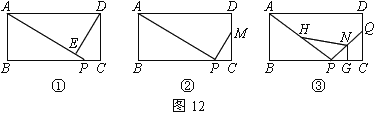
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点E、F,且PA=PD.
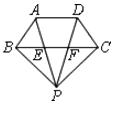
(1)写出三对你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
【答案】(1)△ABP≌△DCP;△ ABE≌△DCF;△BEP≌△CFP;△BFP≌△CEP(2)见解析
【解析】
(1)根据全等三角形的判定方法,正确的去找出图中的全等三角形即可;
(2)选择△ABP≌△DCP给予证明,根据题意可以得出梯形ABCD是等腰梯形,可得∠BAD=∠CDA,△ADP是等腰三角形,可得∠PAD=∠PDA,再结合题目给的已知条件即可证明全等.
解:(1)△ABP≌△DCP;△ ABE≌△DCF;△BEP≌△CFP;△BFP≌△CEP.
(2) 证明:∵AD∥BC,AB=DC,
∴梯形ABCD为等腰梯形,
∴∠BAD=∠CDA.
又∵PA=PD,
∴∠PAD=∠PDA,
∴∠BAD-∠PAD=∠CDA-∠PDA.
即∠BAP=∠CDP.
在△ABP和△DCP中,
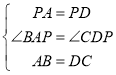
∴△ABP≌△DCP.

【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
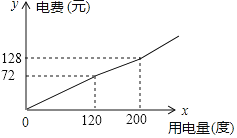
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?