题目内容
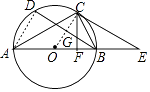
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
【答案】
(1)证明:连接OC,
∵∠A=∠CBD,
∴ ![]() =
= ![]() ,
,
∴OC⊥BD,
∵CE∥BD,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:∵AB为直径,
∴∠ACB=90°,
∵CF⊥AB,
∴∠ACB=∠CFB=90°,
∵∠ABC=∠CBF,
∴∠A=∠BCF,
∵∠A=∠CBD,
∴∠BCF=∠CBD,
∴CG=BG;
(3)解:连接AD,
∵AB为直径,
∴∠ADB=90°,
∵∠DBA=30°,
∴∠BAD=60°,
∵ ![]() =
= ![]() ,
,
∴∠DAC=∠BAC= ![]() ∠BAD=30°,
∠BAD=30°,
∴ ![]() =tan30°=
=tan30°= ![]() ,
,
∵CE∥BD,
∴∠E=∠DBA=30°,
∴AC=CE,
∴ ![]() =
= ![]() ,
,
∵∠A=∠BCF=∠CBD=30°,
∴∠BCE=30°,
∴BE=BC,
∴△CGB∽△CBE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵CG=4,
∴BC=4 ![]() ,
,
∴BE=4 ![]() .
.
【解析】(1)连接OC,由两弧再根据垂径定理得到OC⊥BD,根据平行线的性质推出OC⊥CE,CE是⊙O的切线;
(2)先根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得CG=BG;
(3)连接AD,根据圆周角定理得和解直角三角形![]() 的值,再根据三角形相似和等腰三角形的判定即可求得BE的值.
的值,再根据三角形相似和等腰三角形的判定即可求得BE的值.
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

 阅读快车系列答案
阅读快车系列答案