题目内容
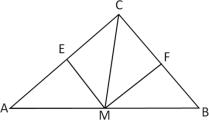
【题目】如图,在![]() 中,
中,![]() ,M是AB中点,
,M是AB中点,![]() ,
,
(1)在AE、EF、FB中是否总有最大的线段?若有,是哪一条?
(2)AE、EF、FB能否构成直角三角形?若能,请加以证明.
【答案】(1)在AE、EF、FB中总有最大的线段,最大的线段是EF;(2)AE、EF、FB能构成直角三角形.
【解析】
(1)过点A作AN∥BC,交FM延长线于点N,连接EN、EF,通过证明△AMN≌△BMF得到NA=FB,NM=FM,结合![]() 可得EN=EF,在Rt△AEN中即可说明最大的线段是EF;
可得EN=EF,在Rt△AEN中即可说明最大的线段是EF;
(2)由(1)可得△AEN为直角三角形且NA=FB,EN=EF,问题得解.
解:(1)在AE、EF、FB中总有最大的线段,最大的线段是EF;
理由:过点A作AN∥BC,交FM延长线于点N,连接EN、EF,
∵AN∥BC,
∴∠NAE=∠ACB=90°,∠NAM=∠B,
在△AMN和△BMF中, ,
,
∴△AMN≌△BMF(ASA),
∴NA=FB,NM=FM,
∵![]() ,
,
∴EN=EF,
∴在Rt△AEN中,斜边EN最长,即在AE、EF、FB中,总有最大的线段EF;
(2)AE、EF、FB能构成直角三角形;
证明:由(1)可知△AEN为直角三角形且NA=FB,EN=EF,
∴AE、EF、FB能构成直角三角形.


练习册系列答案
相关题目