题目内容
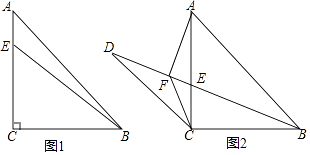
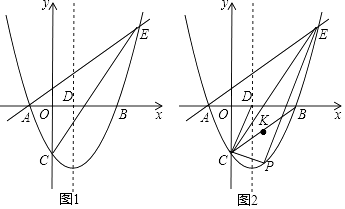
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

【答案】(1)BF=AC,理由见解析;(2)NE=![]() AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=![]() AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵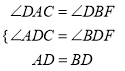 ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=![]() AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=![]() AC.
AC.

练习册系列答案
相关题目