题目内容
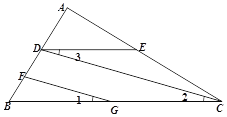
【题目】如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.

【答案】详见解析.
【解析】
根据已知条件证明AB=CD,AF=CF,证明 Rt△ABF≌Rt△CDE(HL),得BF=DE,进而证明△BFG≌△DEG(AAS),即可证明.
证明∵DE⊥AC,BF⊥AC,
∴∠DEG=∠BFE=90°,
∵AE=CF,AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,AB=CD,AF=CF,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中,∠BFG=∠DEG,∠BGF=∠DGE,BF=DE
∴△BFG≌△DEG(AAS),
∴FG=EG,即BD平分EF

练习册系列答案
相关题目
【题目】下表是根据对初一(1)班的50名同学平时最爱吃的食物的种类进行的问卷调查绘制成的统计表,请填满缺少的项并回答后面的问题.
肉类 | 蔬菜类 | 瓜果类 | 水产类 | |
男生 | 22 | 1 | 2 | |
女生 | 4 | 5 | 3 | |
频率 | 64% | 14% | 12% |
(1)选择适当的统计图表示男生平时最爱吃的食物的种类情况;
(2)就给出的初一(1)班的同学平时最爱吃的食物的种类情况,请你结合自己的年龄特点简略谈谈自己的看法.